
分析 由题意,$\frac{1}{2}•2a•a•sinA$=1,sinA=$\frac{1}{{a}^{2}}$,求BC最短时k的值,考虑A为锐角或直角时即可,求出BC,利用导数知识,即可求解.
解答 解:由题意,$\frac{1}{2}•2a•a•sinA$=1,∴sinA=$\frac{1}{{a}^{2}}$,
求BC最短时k的值,考虑A为锐角或直角时即可,∴cosA=$\frac{\sqrt{{a}^{2}-1}}{{a}^{2}}$,
∴由余弦定理可得BC2=5a2-4$\sqrt{{a}^{4}-1}$,
设a2=t>0,则f(t)=5t-4$\sqrt{{t}^{2}-1}$,
f′(t)=5-$\frac{4t}{\sqrt{{t}^{2}-1}}$,
t>$\frac{5}{3}$,f′(t)>0,函数单调递增,0<t<$\frac{5}{3}$,f′(t)<0,函数单调递减,
∴t=$\frac{5}{3}$时,函数f(t)取得最小值,即BC=$\sqrt{3}$,
∴cosA=$\frac{4}{5}$=2cos2∠CAD-1,∴cos∠CAD=$\frac{3\sqrt{10}}{10}$,
∴k=$\frac{4}{3}$cos∠CAD=$\frac{2\sqrt{10}}{5}$.
故答案为:$\frac{2\sqrt{10}}{5}$.
点评 本题考查余弦定理的运用,考查导数知识,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
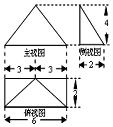
| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间(0,1)内有零点,在区间(1,+∞)内无零点 | |
| B. | 在区间(0,1)内有零点,在区间(1,+∞)内有零点 | |
| C. | 在区间(0,3),(3,+∞)均无零点 | |
| D. | 在区间(0,3),(3,+∞)均有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
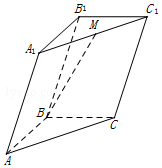
| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com