
(本小题满分13分)某市“环保提案”对某处的环境状况进行了实地调研,据测定,该处的污染指数与附近污染源的强度成正比,与到污染源的距离成反比,比例常数为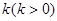 .现已知相距
.现已知相距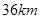 的
的 ,
, 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数 ,
, ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数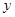 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设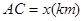 .
.
(1) 试将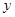 表示为
表示为 的函数;
的函数;
(2) 若 时,
时,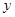 在
在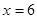 处取得最小值,试求
处取得最小值,试求 的值.
的值.
(1)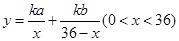 (2)
(2)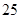
解析试题分析:(1)设点C受A污染源污染指数为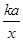 ,
,
点C受B污染源污染指数为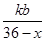 ,
,
其中k为比例系数,且k>0,
从而点C处污染指数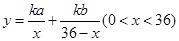 . ……5分
. ……5分
(2) 因为 ,所以,
,所以,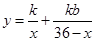 ,
,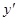 =
=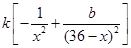 ,
,
令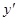 =0,得
=0,得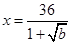 ,
,
当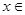
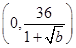 时,函数单调递减;当
时,函数单调递减;当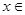
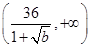 时,函数单调递增.
时,函数单调递增.
∴当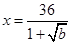 时,函数取得最小值,又此时
时,函数取得最小值,又此时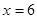 ,解得
,解得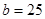 ,
,
经验证符合题意.
所以,污染源B的污染强度 的值为
的值为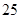 . ……13分
. ……13分
考点:本小题主要考查利用导数求解实际问题中的最值问题,考查了学生从实际问题向数学问题转化的能力和分类讨论思想的应用以及运算求解能力.
点评:从实际问题中抽象数学模型时,一定不要忘记函数的实际定义域,利用导数研究函数的单调性时,要把单调性说清楚,必要时可以画表格辅助说明.


科目:高中数学 来源: 题型:解答题
为了应对国际原油的变化,某地建设一座油料库。现在油料库已储油料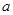 吨,计划正式运营后的第一年进油量为已储油量的
吨,计划正式运营后的第一年进油量为已储油量的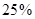 ,以后每年的进油量为上一年年底储油量的
,以后每年的进油量为上一年年底储油量的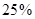 ,且每年运出
,且每年运出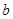 吨,设
吨,设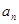 为正式运营第n年年底的储油量。(其中
为正式运营第n年年底的储油量。(其中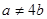 )
)
(1)求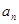 的表达式
的表达式
(2)为应对突发事件,该油库年底储油量不得少于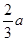 吨,如果
吨,如果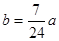 吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取
吨,该油库能否长期按计划运营?如果可以请加以证明;如果不行请求出最多可以运营几年。(取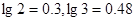 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知函数
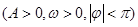 ,在同一周期内,
,在同一周期内,
当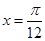 时,
时, 取得最大值
取得最大值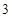 ;当
;当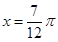 时,
时, 取得最小值
取得最小值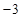 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)若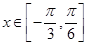 时,函数
时,函数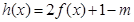 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义:若函数 对于其定义域内的某一数
对于其定义域内的某一数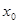 ,有
,有 ,则称
,则称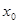 是
是 的一个不动点. 已知函数
的一个不动点. 已知函数 .
.
(1)当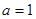 ,
,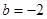 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意的实数b,函数 恒有两个不动点,求实数
恒有两个不动点,求实数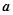 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的不动点,且线段AB的中点C在函数
的不动点,且线段AB的中点C在函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.
(参考公式:若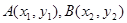 ,则线段AB的中点坐标为
,则线段AB的中点坐标为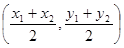 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com