
(12分)已知函数
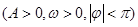 ,在同一周期内,
,在同一周期内,
当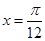 时,
时, 取得最大值
取得最大值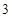 ;当
;当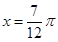 时,
时, 取得最小值
取得最小值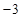 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)若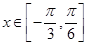 时,函数
时,函数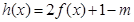 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分13分)
已知函数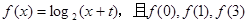 成等差数列,点
成等差数列,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点 关于原点的对称点
关于原点的对称点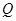 的轨迹是函数
的轨迹是函数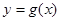 的图像。
的图像。
(1)解关于 的不等式
的不等式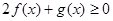 ;
;
(2)当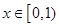 时,总有
时,总有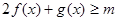 恒成立,求
恒成立,求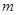 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)某市“环保提案”对某处的环境状况进行了实地调研,据测定,该处的污染指数与附近污染源的强度成正比,与到污染源的距离成反比,比例常数为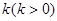 .现已知相距
.现已知相距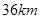 的
的 ,
, 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数 ,
, ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数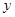 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设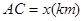 .
.
(1) 试将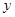 表示为
表示为 的函数;
的函数;
(2) 若 时,
时,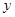 在
在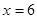 处取得最小值,试求
处取得最小值,试求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12)
为了绿化城市,准备在如图所示的区域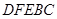 内修建一个矩形
内修建一个矩形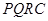 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且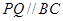 ,
,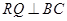 ,另外
,另外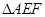 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量 ,
,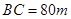 ,
, 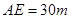 ,
,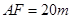 .
.
(1)求直线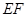 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。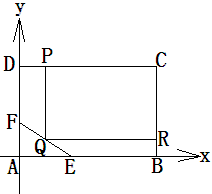
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com