
(本小题满分12分)
已知函数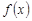 =
=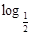 (ex-1)。
(ex-1)。
(1)求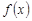 的定义域;
的定义域;
(2)判断函数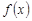 的增减性,并用定义法证明.
的增减性,并用定义法证明.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题满分16分)
如图,开发商欲对边长为 的正方形
的正方形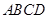 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路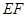 (点
(点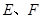 分别在
分别在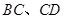 上),根据规划要求
上),根据规划要求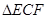 的周长为
的周长为 .
.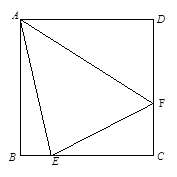
(1)设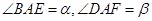 ,求证:
,求证: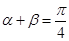 ;
;
(2)欲使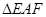 的面积最小,试确定点
的面积最小,试确定点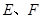 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对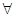 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe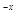 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知函数
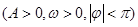 ,在同一周期内,
,在同一周期内,
当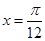 时,
时, 取得最大值
取得最大值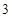 ;当
;当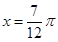 时,
时, 取得最小值
取得最小值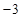 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)若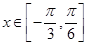 时,函数
时,函数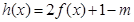 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
武汉市某地西瓜从2012年6月1日起开始上市。通过市场调查,得到西瓜种植成本Q(单位:元/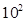 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表:
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
 , Q= a
, Q= a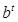 , Q=a
, Q=a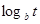 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com