
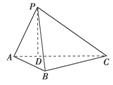
如图所示,在三棱锥P- ABC
ABC 中,AB=BC=
中,AB=BC=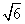 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=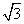 .
.
(1)证明:△PBC为直角三角形;
(2)求直线AP与平面PBC所成角的正弦值.
解:

(1)证明:因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD⊂平面PAC,PD⊥AC,
所以PD⊥平面ABC.
记AC边上的中点为E,在△ABC中,
AB=BC,所以BE⊥AC.
因为AB=BC=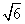 ,AC=4,
,AC=4,
所以BE=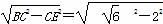 =
=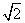 .
.
因为PD⊥AC,所以△PCD为直角三角形.
因为PD=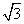 ,CD=3,
,CD=3,
所以PC=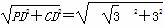 =2
=2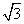 .
.
连接BD,在Rt△BDE中,因为BE=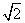 ,DE=1,
,DE=1,
所以BD= =
=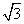 .
.
因为PD⊥平面ABC,BD⊂平面ABC,所以PD⊥BD.
在Rt△PBD中,因为PD=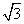 ,BD=
,BD=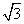 ,
,
所以PB=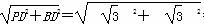 =
=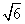 .
.
在△PBC中,因为BC=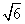 ,PB=
,PB=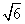 ,PC=2
,PC=2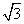 ,
,
所以BC2+PB2=PC2,
即△PBC为直角三角形.
(2)
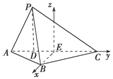
以点E为坐标原点,以EB,EC所在的直线分别为x轴,y轴建立如图的空间直角坐标系Exyz,
则A(0,-2,0),B(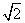 ,0,0),C(0,
,0,0),C(0, 2,0),P(0,-1,
2,0),P(0,-1,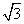 ).
).
于是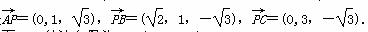
设平面PBC的法向量为n=(x,y,z),
则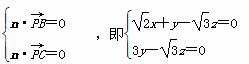
取y=1,则z=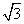 ,x=
,x=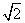 ,
,
所以平面PBC的一个法向量为n=(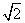 ,1,
,1,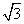 ).
).
设直线AP与平面PBC所成的角为θ,
则sinθ=|cos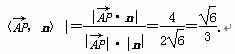
所以直线AP与平面PBC所成角的正弦值为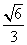 .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
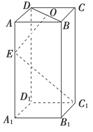
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.
(1)证明:BD⊥EC1;
(2)如果AB=2,AE=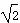 ,OE⊥EC1,求AA1的长
,OE⊥EC1,求AA1的长 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=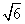 ,M是CC1的中点,则异面直线AB1与A1M所成的角为( )
,M是CC1的中点,则异面直线AB1与A1M所成的角为( )
A.60° B.45°
C.30° D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点E、F分别在正方体ABCDA1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校高一、高二、 高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年
高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年 级抽取________名学生.
级抽取________名学生.
查看答案和解析>>
科目:高中数学 来源: 题型:
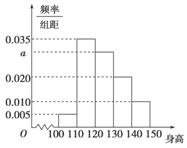
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=______.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com