
| A. | (-3,3) | B. | (-4,4) | C. | (-5,5) | D. | [-5,5] |
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:填空题
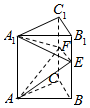 如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,设三棱锥A1-AEF和四棱锥A-BCFE的体积分别为V1,V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{6}{7}$.
如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,设三棱锥A1-AEF和四棱锥A-BCFE的体积分别为V1,V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{6}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<1} | B. | {x|x<0} | C. | C{x|x≥0} | D. | {x|x>0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
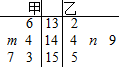 甲、乙两市各五个镇民政局在2016年2月14日当天领取结婚证新人的对数如茎叶图所示,已知甲市的数据的中位数为145,乙市的数据的平均数为145,则m+n=10.
甲、乙两市各五个镇民政局在2016年2月14日当天领取结婚证新人的对数如茎叶图所示,已知甲市的数据的中位数为145,乙市的数据的平均数为145,则m+n=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com