
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 过P作a′∥a,b′∥b,设直线a′、b′确定的平面为α,异面直线a、b成60°角,直线a′、b′所成锐角为60°,过点P与a′、b′都成60°角的直线,可以作3条.
解答 解:过P作a′∥a,b′∥b,
设直线a′、b′确定的平面为α,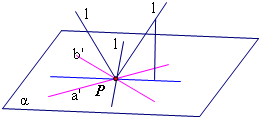
∵异面直线a、b成60°角,
∴直线a′、b′所成锐角为60°.
①当直线l在平面α内时,
若直线l平分直线a′、b′所成的钝角,
则直线l与a、b都成60°角;
②当直线l与平面α斜交时,若它在平面α内的射影恰好落在直线a′、b′所成的锐角平分线上时,直线l与a、b所成角相等.
此时l与a′、b′所成角的范围为[30°,90°],适当调整l的位置,可使直线l与a、b也都成60°角,这样的直线l有两条.
综上所述,过点P与a′、b′都成60°角的直线,可以作3条.
∵a′∥a,b′∥b,∴过点P与a′、b′都成60°角的直线,与a、b也都成60°的角.
故选:C.
点评 本题考查了空间位置关系、空间角,考查了作图能力、空间想象能力,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 若命题p、q中至少有一个为真命题,则“p∧q”是真命题 | |
| B. | 不等式ac2>bc2成立的充要条件是a>b | |
| C. | “正四棱锥的底面是正方形”的逆命题是真命题 | |
| D. | 若k>0,则方程x2+2x-k=0有实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx4,g(x)=4lgx | B. | $f(x)=\left\{\begin{array}{l}x,x≥0\\-x,x<0\end{array}\right.$,$g(x)=\sqrt{x^2}$ | ||
| C. | $f(x)=\frac{{{x^2}-4}}{x-2}$,g(x)=x+2 | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1}$,$g(x)=\sqrt{{x^2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
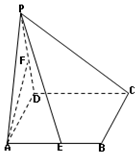 已知:四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点,PA=a,∠PDA=45°
已知:四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点,PA=a,∠PDA=45°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{{x^2}+x}}{x+1}$与g(x)=x-1 | B. | f(x)=2|x|与$g(x)=\sqrt{4{x^2}}$ | ||
| C. | $f(x)=\sqrt{x^2}$与$g(x)={(\sqrt{x})^2}$ | D. | $y=\sqrt{x+1}\sqrt{x-1}$与$y=\sqrt{{x^2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com