
| A. | 若命题p、q中至少有一个为真命题,则“p∧q”是真命题 | |
| B. | 不等式ac2>bc2成立的充要条件是a>b | |
| C. | “正四棱锥的底面是正方形”的逆命题是真命题 | |
| D. | 若k>0,则方程x2+2x-k=0有实根 |
分析 由复合命题的真假判断判断A;由充分必要条件的判断方法判断B;写出原命题的逆命题判断C;由方程x2+2x-k=0得判别式大于0说明D正确.
解答 解:对于A,命题p、q均为真命题,则“p∧q”是真命题,故A错误;
对于B,由a>b,不一定有ac2>bc2,反之,由ac2>bc2,一定有a>b.
∴不等式ac2>bc2成立的必要不充分条件是a>b,故B错误;
对于C,“正四棱锥的底面是正方形”的逆命题是“底面是正方形的四棱锥是正四棱锥”,是假命题,故C错误;
对于D,若k>0,则方程x2+2x-k=0的判别式△=4+4k>0,方程有实根,故D正确.
点评 本题考查命题的真假判断与应用,考查了复合命题的真假判断,考查充分必要条件的判断方法,是基础题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
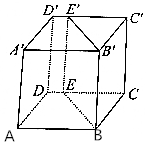 如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )
如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则a2>b2 | B. | 若a>|b|,则a2>b2 | C. | 若|a|>b,则a2>b2 | D. | 若|a|≠b,则a2≠b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com