练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．过点M（1，-2）的直线l将圆C：（x-2）2+y2=9分成两段弧，当其中的劣弧最短时，直线l的方程是x+2y+3=0．

    分析 根据垂径定理得到过M的弦最短时，所对的劣弧最短，而当直线l与直线AM垂直时得到的弦最短，根据两直线垂直时斜率乘积为-1得到直线l的斜率，写出直线l的方程即可．

    解答 解：当劣弧最短时，MA与直线l垂直．所以kl•kAM=-1，圆心坐标为（2，0）得到直线AM的斜率kAM=2，
    所以kl=-$\frac{1}{2}$
    所以过M（1，-2）的直线l的方程为：y+2=-$\frac{1}{2}$（x-1）化简得x+2y+3=0．
    故答案为：x+2y+3=0．

    点评 考查学生灵活运用垂径定理解决数学问题的能力，掌握两直线垂直时所取的条件是斜率乘积等于-1，会根据条件写出直线的一般式方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．已知a，b是正数，且a≠b，比较a3+b3与a2b+ab2的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．化简求值：
    （1）（7+4$\sqrt{3}$）${\;}^{\frac{1}{2}}}$-81${\;}^{\frac{1}{8}}}$+32${\;}^{\frac{3}{5}}}$-2×（$\frac{1}{8}$）${\;}^{-\frac{2}{3}}}$+$\root{3}{2$×（4${\;}^{-\frac{1}{3}}}$）-1
    （2）（log62）2+（log63）2+3log62×（log6$\root{3}{18}$-$\frac{1}{3}$log62）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．函数y=x+$\frac{9}{x+1}$（x≠-1）的值域为（-∞，-7]∪[5，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知等差数列{an}中，a1=-3，11a5=5a8，前n项和为Sn．
    （1）求an；
    （2）当n为何值时，Sn最小？并求Sn的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．下列判断正确的是（　　）
    A．若命题p、q中至少有一个为真命题，则“p∧q”是真命题
    B．不等式ac2＞bc2成立的充要条件是a＞b
    C．“正四棱锥的底面是正方形”的逆命题是真命题
    D．若k＞0，则方程x2+2x-k=0有实根

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．某几何体的三视图如图所示，则该几何体的体积为（　　）
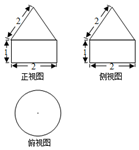
    A．$π+\sqrt{3}π$B．$\frac{4}{3}π$C．$2π+\frac{{2\sqrt{3}}}{3}π$D．$π+\frac{{\sqrt{3}}}{3}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列四组函数中，表示同一函数的是（　　）
    A．f（x）=lgx4，g（x）=4lgxB．$f（x）=\left\{\begin{array}{l}x，x≥0\\-x，x＜0\end{array}\right.$，$g（x）=\sqrt{x^2}$
    C．$f（x）=\frac{{{x^2}-4}}{x-2}$，g（x）=x+2D．$f（x）=\sqrt{x+1}•\sqrt{x-1}$，$g（x）=\sqrt{{x^2}-1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．（1）已知全集U={x|-5≤x≤10，x∈Z}，集合M={x|0≤x≤7，x∈Z}，N={x|-2≤x＜4，x∈Z}，求（∁UN）∩M（分别用描述法和列举法表示结果）
    （2）已知全集U=A∪B={0，1，2，3，4，5，6，7，8，9，10}，若集合A∩∁UB={2，4，6，8}，求集合B；
    （3）已知集合P={x|ax2+2ax+1=0，a∈R，x∈R}，当集合P只有一个元素时，求实数a的值，并求出这个元素．

    查看答案和解析>>

    同步练习册答案