
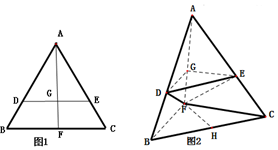
分析 (1)运用面面平行的判定定理,可先证DG∥平面BCF,EG∥平面BCF,即可得到;
(2)连接EH,运用中位线定理可得异面直线AB与FH所成角即为∠FHE,再由直角三角形的性质和余弦定理,即可得到所求值.
解答 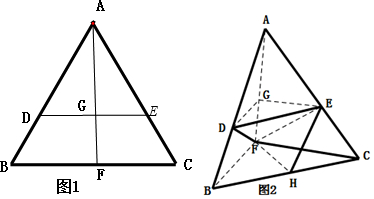 证明:(1)如题图1,在等边三角形ABC中,AB=AC,
证明:(1)如题图1,在等边三角形ABC中,AB=AC,
∵AD=AE,∴$\frac{AD}{DB}=\frac{AE}{EC}$,
∴DE∥BC,∴DG∥BF,
如题图2,∵DG?平面BCF,
∴DG∥平面BCF,…(2分)
同理可证EG∥平面BCF,
∵DG∩EG=G,
∴平面DEG∥平面BCF…(4分)
解:(2)连EH,
∵EH是△CAB的中位线,
∴$EH∥AB,EH=\frac{1}{2}AB=\frac{1}{2}$
∴异面直线AB与FH所成角即为∠FHE…(6分)
∵$在△BCF中BF=FC=\frac{1}{2},BC=\frac{{\sqrt{2}}}{2}$
∴△BFC为RT△,∴$FH=\frac{{\sqrt{2}}}{4}$,
又∵$FE=\frac{1}{2}$
∴cos∠FHE=$\frac{F{H}^{2}+E{H}^{2}-E{F}^{2}}{2FH•EH}$=$\frac{\frac{1}{4}+\frac{2}{16}-\frac{1}{4}}{2×\frac{1}{2}×\frac{\sqrt{2}}{4}}$=$\frac{\sqrt{2}}{4}$…(8分)
点评 本题考查面面平行的证明和异面直线所成角的求法,注意运用线面平行的判定定理和平移法,考查空间想象能力和推理及计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p、q中至少有一个为真命题,则“p∧q”是真命题 | |
| B. | 不等式ac2>bc2成立的充要条件是a>b | |
| C. | “正四棱锥的底面是正方形”的逆命题是真命题 | |
| D. | 若k>0,则方程x2+2x-k=0有实根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com