
分析 (1)利用指数函数的单调性,对底数a讨论,即可单调性.
(2)令f(x)+g(x)-2=h(x).证明其奇偶性,利用奇偶性求值.
(3)利用(1)(2)中的结论,将不等式转化为二次函数恒成立问题,即可求解t的取值范围.
解答 解:(1)由题意:函数f(x)=$\frac{a}{{a}^{2}-1}$(a-x-ax),
①当0<a<1时,$f(x)=\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})$递减,
②当a>1时,$f(x)=\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})$递减,
∴当且a>0且a≠1时,f(x)是减函数.
(2)由题意g(x)=-ax+2.
设h(x)=f(x)+g(x)-2,则:h(x)=$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})-ax$,其定义域为R,关于原点对称,
h(-x)=$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{-x}}-{a}^{-x})+ax$=$\frac{a}{{a}^{2}-1}({a}^{x}-\frac{1}{{a}^{x}})+ax$=-[$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})-ax$]=-h(x)
∵h(-x)=-h(x),
∴h(x)是定义域为R的奇函数.
∵g(2)+f(2)=3,则:h(2)=1,
∴h(-2)=-1,即:g(2)+f(2)-2=-1
所以g(2)+f(2)=1.
(3)由(2)知h(x)是定义域为R的奇函数,且在R上为减函数,
由h(x2+tx)+h(4-x)<0,则有:h(x2+tx)<h(-4+x)
∴x2+tx>x-4,即x2+(t-1)x+4>0 恒成立,
∴△=b2-4ac=(t-1)2-16<0
解得:-3<t<5,
故得t的取值范围是(-3,5).
点评 本题考查了复合函数的单调性和构造函数思想利用奇偶性求值,将恒等式问题转化为不等式求解,综合性强,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+ax+1,a∈R | B. | f(x)=x+2a-1,a∈R | ||
| C. | f(x)=log2(ax2-1),a∈R | D. | f(x)=(x-a)|x|,a∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
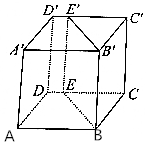 如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )
如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com