
 +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f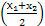 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”. +alnx,
+alnx,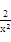 +
+ .
.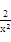 +
+ ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立. -2x2在[1,+∞)上恒成立.
-2x2在[1,+∞)上恒成立. -2x2,上述问题等价于a≥φ(x)max,而φ(x)=
-2x2,上述问题等价于a≥φ(x)max,而φ(x)= -2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.
-2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求. +alnx得
+alnx得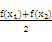 =
= (
(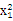 +
+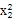 )+
)+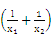 +
+ (lnx1+lnx2)
(lnx1+lnx2) (
(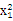 +
+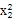 )+
)+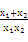 +aln
+aln ,
,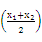 =
=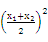 +
+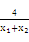 +aln
+aln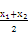 ,
, (
(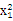 +
+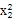 )≥
)≥ [(
[(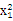 +
+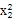 )+2x1x2]=
)+2x1x2]=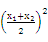 , ①
, ①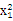 +
+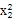 )+2x1x2≥4x1x2,
)+2x1x2≥4x1x2,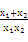 ≥
≥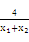 . ②
. ② ≤
≤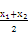 ,所以ln
,所以ln ≤ln
≤ln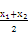 ,
, ≥aln
≥aln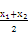 , ③
, ③ (
(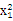 +
+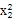 )+
)+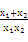 +aln
+aln ≥
≥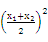 +
+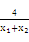 +aln
+aln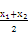 ,
,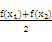 ≥f
≥f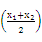 ,
,

科目:高中数学 来源:不详 题型:解答题
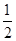 ,-
,-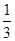 ]上有单调递增区间?
]上有单调递增区间?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于 的近似函数关系式为
的近似函数关系式为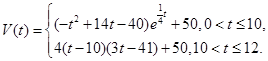
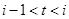 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期? 计算).
计算).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com