
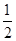 ,-
,-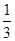 ]上有单调递增区间?
]上有单调递增区间?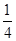 (2)a∈(-1,+∞).
(2)a∈(-1,+∞).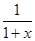 -2ax-1=
-2ax-1=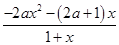 ,
,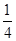 ,
,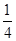 时,f′(x)=
时,f′(x)= =
=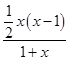 ,
,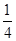 .
.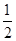 ,-
,-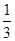 ]上有单调递增区间,
]上有单调递增区间,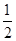 ,-
,-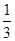 ]上有解,
]上有解,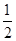 ≤x≤-
≤x≤-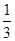 时,
时,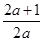 ,
,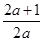 <-
<-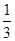 ,
,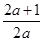 ,
,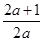 >-
>-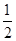 ,
,

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f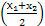 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.[1,+∞) | B.[1,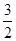 ) ) | C.[1,2) | D.[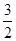 ,2) ,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com