
分析 (1)由题意易得周期为π,可得ω,再由对称轴可得φ值,可得解析式;
(2)由三角函数图象变换真假求解函数的解析式即可.
(3)借助正弦函数的单调增区间求解函数的单调减区间即可.
解答 解:(1)∵函数f(x)图象上相邻两个最底点的距离为π,
∴?(x)的最小正周期T=π,∴ω=$\frac{2π}{T}$=2,
又∵f(x)图象关于直线x=$\frac{π}{3}$对称,
∴2×$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,
∵-$\frac{π}{2}$≤φ<$\frac{π}{2}$,∴φ=-$\frac{π}{6}$,
∴f(x)=$\sqrt{3}$sin(2x-$\frac{π}{6}$);
(2)将函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到f(x)=$\sqrt{3}$sin(2x+$\frac{π}{3}$-$\frac{π}{6}$)=$\sqrt{3}$sin(2x+$\frac{π}{6}$);
再将所得图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)=$\sqrt{3}$sin($\frac{1}{2}$x+$\frac{π}{6}$);
x∈[-π,π],$\frac{1}{2}$x+$\frac{π}{6}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
g(x)在[-π,π]上的值域为;[$-\frac{3}{2}$,$\sqrt{3}$].
(3)g(x)=$\sqrt{3}$sin($\frac{1}{2}$x+$\frac{π}{6}$);
∵$\frac{π}{3}≤x≤\frac{10π}{3}$,∴$\frac{π}{3}≤\frac{1}{2}x+\frac{π}{6}≤\frac{11π}{6}$,当$\frac{π}{3}≤\frac{1}{2}x+\frac{π}{6}≤\frac{π}{2}$,即:$\frac{π}{3}≤x≤\frac{2π}{3}$时,g(x)单调递增,
当$\frac{3π}{2}≤\frac{1}{2}x+\frac{π}{6}≤\frac{11π}{6}$,即$\frac{8π}{3}≤x≤\frac{10π}{3}$时g(x)单调递增.
∴g(x)在[$\frac{π}{3}$,$\frac{10π}{3}$]上的单调递增区间:[$\frac{π}{3}$,$\frac{2π}{3}$],[$\frac{8π}{3}$,$\frac{10π}{3}$].
点评 本题考查三角函数的图象和性质,涉及三角函数的对称性和最值,三角函数的平移变换,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
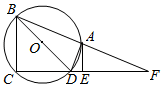 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,直线CD与直线AB交于点F,E在DF上,AE是⊙O的切线,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,直线CD与直线AB交于点F,E在DF上,AE是⊙O的切线,DA平分∠BDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{3}$,+∞) | C. | ($\sqrt{2}$+1,+∞) | D. | ($\sqrt{3}$+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 中国十佳宜居城市 | 中国十佳最美丽城市 | ||||
| 排名 | 城市 | 得分 | 排名 | 城市 | 得分 |
| 1 | 深圳 | 90.2 | 1 | 杭州 | 93.7 |
| 2 | 珠海 | 89.8 | 2 | 拉萨 | 93.5 |
| 3 | 烟台 | 88.3 | 3 | 深圳 | 93.3 |
| 4 | 惠州 | 86.5 | 4 | 青岛 | 92.2 |
| 5 | 信阳 | 83.1 | 5 | 大连 | 92.0 |
| 6 | 厦门 | 81.4 | 6 | 银川 | 91.9 |
| 7 | 金华 | 79.2 | 7 | 惠州 | 90.6 |
| 8 | 柳州 | 77.8 | 8 | 哈尔滨 | 90.3 |
| 9 | 扬州 | 75.9 | 9 | 信阳 | 89.3 |
| 10 | 九江 | 74.6 | 10 | 烟台 | 88.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
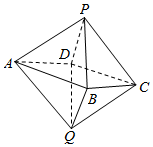 甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.
甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com