
分析 (1)根据题意,算出f(x)的周期T,结合周期公式解得ω,再结合y取最大值1解出φ,即可得到函数的解析式;
(2)直接利用三角函数图象的变换,求解三角函数即可.
(3)由(1)的结论,得函数在[0,$\frac{8π}{3}$]内恰有4个周期,根据正弦函数图象的对称性,得到在[0,$\frac{8π}{3}$]内有6个根且分别关于直线x=$\frac{π}{4}$、x=$\frac{11π}{12}$和x=$\frac{19π}{12}$和x=$\frac{27π}{12}$对称,由此加以计算即可得到所有实数根之和.
解答 解:(1)由题意,得:
周期T=$\frac{2π}{ω}$=2($\frac{7π}{12}$-$\frac{π}{4}$),解得ω=3,
又∵当x=$\frac{π}{4}$时y取最大值1,
∴sin($\frac{3π}{4}$+φ)=1,结合|φ|<$\frac{π}{2}$可得φ=-$\frac{π}{4}$,
因此函数的解析式为f(x)=sin(3x-$\frac{π}{4}$);
(2)函数y=sinx的图象向右平移$\frac{π}{4}$单位,得到y=sin(x-$\frac{π}{4}$),再把函数图象上的点的横坐标变为原来的$\frac{1}{3}$,得到f(x)=sin(3x-$\frac{π}{4}$)的图象.
(3)∵f(x)=sin(3x-$\frac{π}{4}$)的周期为$\frac{2π}{3}$,
∴函数在[0,$\frac{8π}{3}$]内恰有4个周期,
并且方程sin(3x-$\frac{π}{4}$)=a,a∈(0,1)在[0,$\frac{8π}{3}$]内有8个实根,
且x1+x2=$\frac{π}{2}$,
同理可得x3+x4=$\frac{11π}{6}$且x5+x6=$\frac{19π}{6}$,x7+x8=$\frac{9π}{2}$.
∴f(x)在[0,$\frac{8π}{3}$]内的所有实数根之和为:$\frac{π}{2}$+$\frac{11π}{6}$+$\frac{19π}{6}$+$\frac{9π}{2}$=10π.
点评 本题给出三角函数图象满足的条件,求函数的表达式并求f(x)在[0,2π]内的所有实数根之和.着重考查了三角函数的周期公式、图象的对称性和最值点对应的自变量等知识,属于中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
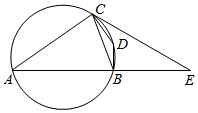 如图,四边形ABDC内接于圆,BD=CD,BD⊥AB,过点C的圆的切线与AB的延长线交于点E,BC=BE,AE=2,则AB=$\sqrt{5}$-1.
如图,四边形ABDC内接于圆,BD=CD,BD⊥AB,过点C的圆的切线与AB的延长线交于点E,BC=BE,AE=2,则AB=$\sqrt{5}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
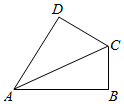 如图,四边形ABCD,∠DAB=60°,CD⊥AD,CB⊥AB.
如图,四边形ABCD,∠DAB=60°,CD⊥AD,CB⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11π}{12}$ | B. | $\frac{π}{12}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 1008 | D. | $\frac{2015}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com