
| A. | 2015 | B. | 2016 | C. | 1008 | D. | $\frac{2015}{2}$ |
分析 根据函数关系,利用倒序相加法进行求解即可.
解答 解:∵函数f(x)满足f(x)+f(2016-x)=1,数列{an}中,an=f(n)(n∈N•),
∴f(n)+f(2016-n)=1,
即an+a2016-n=1,
则数列{an}的前2015项和S2015=a1+a2+a3+…+a2015,
则S2015=a2015+a2014+a2013+…+a2+a1,
两式相加得2S2015=a1+a2+a3+…+a2015+a2015+a2014+a2013+…+a2+a1,
=(a1+a2015)+(a2+a2014)+…+(a2015+a1)=1+1+…+1=2015,
则S2015=$\frac{2015}{2}$,
故选:D
点评 本题主要考查数列求和的计算,根据数列和函数的关系,利用倒序相加法进行求解是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
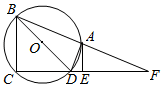 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,直线CD与直线AB交于点F,E在DF上,AE是⊙O的切线,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,直线CD与直线AB交于点F,E在DF上,AE是⊙O的切线,DA平分∠BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 12 | 13 | 14 | 15 | 16 |
| 乙 | 16 | 17 | 18 | 19 | a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
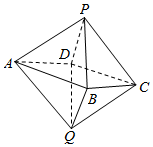 甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.
甲乙两位同学各有一个正八面体((有6个顶点和12条边8个面,它由8个等边三角形构成,如图所示),他们分别从这个八面体的六个顶点任意选取4个,则恰好有一人能将选取的4个点构成一个四面体的概率为$\frac{52}{225}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com