
分析 根据数列的前n项和通项公式之间的关系,即可得到结论.
解答 解:当n=1时,${S_1}={a_1}=\frac{1}{6}{a_1}({a_1}+3)$,解得a1=3;
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{1}{6}[{a_n}({a_n}+3)-{a_{n-1}}({a_{n-1}}+3)]$,
整理,得(an+an-1)(an-an-1-3)=0.
因为an>0,所以an-an-1-3=0,即an-an-1=3,
所以{an}是以3为首项,3为公差的等差数列,所以an=3+3(n-1)=3n,即an=3n.
故答案为:an=3n.
点评 本题主要考查数列通项公式的求解,根据递推关系判断数列是等差数列是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a1a2>0,则a2a3>0 | B. | 若a1a3<0,则a1a2<0 | ||
| C. | 若a1<a2,则a22<a1a3 | D. | 若a1≥a2,则a22≥a1a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N=N | B. | M∩(∁UN)=∅ | C. | M∪N=U | D. | M⊆(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
设 为抛物线
为抛物线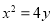 上的两动点,且线段
上的两动点,且线段 的长为6,
的长为6,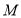 为线段
为线段 的中点,则点
的中点,则点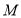 到
到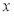 轴的最短距离为 .
轴的最短距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com