
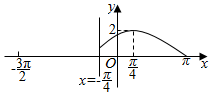 已知定义在区间[-$\frac{3π}{2}$,π]上的函数y=f(x)的图象关于直线x=-$\frac{π}{4}$对称,当x∈[-$\frac{π}{4}$,π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),且其图象如图所示.
已知定义在区间[-$\frac{3π}{2}$,π]上的函数y=f(x)的图象关于直线x=-$\frac{π}{4}$对称,当x∈[-$\frac{π}{4}$,π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),且其图象如图所示.分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数在[-$\frac{π}{4}$,π]上的解析式.再利用利用图象的对称性求函数在∈[-$\frac{3π}{2}$,-$\frac{π}{4}$]上的解析式,从而得出结论.
(2)由条件,分类讨论,分别求得x的值,从而得出结论.
解答 解:(1)由条件根据函数y=f(x)的图象,可得A=2,$\frac{1}{4}•\frac{2π}{ω}$=π-$\frac{π}{4}$,求得ω=$\frac{2}{3}$.
再根据五点法作图,可得$\frac{2}{3}$•$\frac{π}{4}$+φ=$\frac{π}{2}$,求得φ=$\frac{π}{3}$,
故函数f(x)在[-$\frac{π}{4}$,π]上的解析式为f(x)=2sin($\frac{2}{3}$x+$\frac{π}{3}$).
设x∈[-$\frac{3π}{2}$,-$\frac{π}{4}$],根据f(x)的图象关于直线x=-$\frac{π}{4}$对称,则-$\frac{π}{2}$-x∈[-$\frac{π}{4}$,π],
故f(x)=f(-$\frac{π}{2}$-x)=2sin[$\frac{2}{3}$(-$\frac{π}{2}$-x)+$\frac{π}{3}$]=2sin(-$\frac{2}{3}$x)=-2sin$\frac{2}{3}$x,
即当x∈[-$\frac{3π}{2}$,-$\frac{π}{4}$]时,f(x)=-2sin$\frac{2}{3}$x.
综上可得,y=f(x)在区间[-$\frac{3π}{2}$,π]上的表达式为 f(x)=$\left\{\begin{array}{l}{2sin(\frac{2}{3}x+\frac{π}{3}),x∈[-\frac{π}{4},π]}\\{-2sin\frac{2}{3}x,x∈[-\frac{3π}{2},-\frac{π}{4}]}\end{array}\right.$.
(2)①由f(x)=2sin($\frac{2}{3}$x+$\frac{π}{3}$)=$\sqrt{3}$,x∈[-$\frac{π}{4}$,π],
可得$\frac{2}{3}$x+$\frac{π}{3}$∈[$\frac{π}{6}$,π],sin($\frac{2}{3}$x+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
∴$\frac{2}{3}$x+$\frac{π}{3}$=$\frac{π}{3}$ 或 $\frac{2}{3}$x+$\frac{π}{3}$=$\frac{2π}{3}$,求得x=0,或 x=$\frac{π}{2}$.
②由x∈[-$\frac{3π}{2}$,-$\frac{π}{4}$]时,f(x)=-2sin$\frac{2}{3}$x=$\sqrt{3}$,
可得$\frac{2}{3}$x∈[-π,-$\frac{π}{6}$],sin$\frac{2}{3}$x=-$\frac{\sqrt{3}}{2}$,∴$\frac{2x}{3}$=-$\frac{2π}{3}$,或 $\frac{2x}{3}$=-$\frac{π}{3}$,
∴x=-π 或x=-$\frac{π}{2}$.
故当x∈[-$\frac{3π}{2}$,π],可得x=0或$\frac{π}{2}$或-π或-$\frac{π}{2}$,即x的取值集合为{0,$\frac{π}{2}$,-π,-$\frac{π}{2}$ }.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.还考查了利用图象的对称性求函数的解析式,解三角方程,属于中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
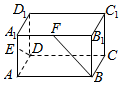 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com