
分析 (1)运用椭圆的定义和直角三角形的勾股定理,结合椭圆的离心率计算即可得到所求值;
(2)由椭圆的离心率和a,b,c的关系,可得椭圆的方程x2+2y2-2c2=0,求得直线AB的方程,代入椭圆方程,运用韦达定理,再由向量的数量积的坐标表示,解方程可得c,进而得到a,b的值,即可得到所求椭圆方程.
解答 解:(1)由椭圆定义可得|MF1|+|MF2|=2a,
∵|MF1|=3|MF2|,∴4|MF2|=2a,
∴$16|M{F_2}{|^2}=4{a^2}$,
在直角△MF2F1中,$|M{F_1}{|^2}-|M{F_2}{|^2}=4{c^2}$,即$8|M{F_2}{|^2}=4{c^2}$,
∴$\frac{{4{c^2}}}{{4{a^2}}}=\frac{1}{2}$,即$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,∴椭圆的离心率为$\frac{{\sqrt{2}}}{2}$;
(2)∵$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,∴$a=\sqrt{2}c,\;b=c$,
∴椭圆方程为$\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$,
即x2+2y2-2c2=0,
易知点M的坐标为$({c,\;\frac{{\sqrt{2}}}{2}c})$,
∵点N是线段MF2的中点,∴点N的坐标为$({0,\;\frac{{\sqrt{2}}}{4}c})$,
∵直线MF1的斜率为$\frac{{\sqrt{2}}}{4}$,∴直线AB的斜率为$-2\sqrt{2}$,
∴直线AB的方程为$y=-2\sqrt{2}x+\frac{{\sqrt{2}}}{4}c$,
与椭圆方程联立消去y得$17{x^2}-4cx-\frac{7}{4}{c^2}=0$,
设点A的坐标为(x1,y1),点B的坐标为(x2,y2),∴${x_1}{x_2}=-\frac{{7{c^2}}}{4×17}$,
∵AB垂直平分线段MF1,∴$\overrightarrow{MA}•\overrightarrow{MB}=\overrightarrow{{F_1}A}•\overrightarrow{{F_1}B}=\frac{27}{17}$,
∴$({{x_1}-c,\;{y_1}-\frac{{\sqrt{2}}}{2}c})•({{x_2}-c,\;{y_2}-\frac{{\sqrt{2}}}{2}c})=\frac{27}{17}$,
∴$({{x_1}-c,\;-2\sqrt{2}{x_1}-\frac{{\sqrt{2}}}{4}c})•({{x_2}-c,\;-2\sqrt{2}{x_2}-\frac{{\sqrt{2}}}{4}c})=\frac{27}{17}$,
∴$({{x_1}-c})({{x_2}-c})+({-2\sqrt{2}{x_1}-\frac{{\sqrt{2}}}{4}c})({-2\sqrt{2}{x_2}-\frac{{\sqrt{2}}}{4}c})=\frac{27}{17}$,
化简得${x_1}{x_2}+\frac{1}{8}{c^2}=\frac{3}{17}$,即$-\frac{{7{c^2}}}{4×17}+\frac{1}{8}{c^2}=\frac{3}{17}$,即为c2=8,
可得a2=2c2=16,b2=c2=8,
则椭圆的方程为$\frac{x^2}{16}+\frac{y^2}{8}=1$.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的定义和勾股定理,考查椭圆方程的求法,注意运用直线方程和椭圆方程联立,运用韦达定理,同时考查向量数量积的坐标表示,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
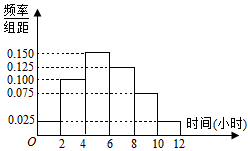 为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,$\frac{7}{16}$] | B. | [-4,1] | C. | [$\frac{1}{4}$,$\frac{7}{16}$] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,+∞) | B. | (-∞,$\frac{1}{3}$) | C. | (-3,$\frac{1}{3}$) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com