
分析 (1)根据两角和的正切公式,把所给的等式的右边展开,利用特殊角的三角函数最后得到和右边的式子相等,等式得证.
(2)猜想是周期函数,利用周期函数的定义证明即可.
解答 解:(1)证明:tan(x+$\frac{π}{4}$)=$\frac{tanx+tan\frac{π}{4}}{1-tanxtan\frac{π}{4}}$=$\frac{1+tanx}{1-tanx}$;
(2)猜想f(x)是以4为周期的周期函数.
证明:因为f(x+2×$\frac{1}{2}$)=f[(x+$\frac{1}{2}$)+$\frac{1}{2}$]=$\frac{1+f(x+\frac{1}{2})}{1-f(x+\frac{1}{2})}$=$\frac{1+\frac{1+f(x)}{1-f(x)}}{1-\frac{1+f(x)}{1-f(x)}}$=-$\frac{1}{f(x)}$,
所以f(x+4)=f[(x+2)+2]=-$\frac{1}{f(x+2)}$=f(x),
所以f(x)是以4为周期的周期函数.
点评 本题考查三角函数的化简求值,周期的应用,基本知识的考查.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
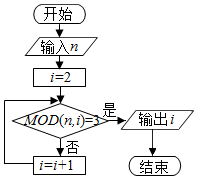 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(7,3)=1,如图是一个算法的程序框图,当输入的n值为15时,输出的结果为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com