
分析 (1)求出圆心到直线的距离与半径比较,即可得出结论;
(2)由题意过圆心(-1,1)与直线x-y-4=0垂直的直线方程为x+y=0,所求的圆的圆心在此直线上,所求的圆的半径为$\sqrt{2}$,即可求出所求圆的方程.
解答 解:(1)圆C:x2+y2+2x-2y=0,可化为(x+1)2+(y-1)2=2,
∴圆x2+y2+2x-2y=0的圆心为(-1,1),半径为$\sqrt{2}$,
圆心到直线的距离d=$\frac{|-1-1-4|}{\sqrt{2}}$=3$\sqrt{2}$>$\sqrt{2}$,
∴直线l与圆C相离;
(2)由题意,过圆心(-1,1)与直线x-y-4=0垂直的直线方程为x+y=0,
所求的圆的圆心在此直线上,
又圆心(-1,1)到直线x-y-4=0的距离为d=$\frac{|-1-1-4|}{\sqrt{2}}$=3$\sqrt{2}$,
则所求的圆的半径为$\sqrt{2}$,
设所求圆心坐标为(a,b)
则$\frac{|a-b-4|}{\sqrt{2}}$=$\sqrt{2}$,且a+b=0
解得a=1,b=-1,
∴与直线l和圆C都相切的半径最小的圆的方程为(x-1)2+(y+1)2=2
点评 本题是中档题,考查直线与圆的位置关系,数形结合的思想,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (${\frac{1}{e}$,+∞) | C. | (${\frac{1}{e}$,e) | D. | (0,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患慢性气管炎 | 未患慢性气管炎 | 总计 | |
| 吸烟 | s | 30 | 100 |
| 不吸烟 | 35 | t | 100 |
| 合计 | 105 | 95 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
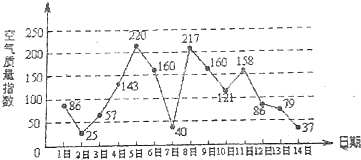 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
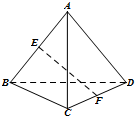 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com