
分析 (1)由an+2=2an+1-an+2,变形为(an+2-an+1)-(an+1-an)=2,a2-a1=4,即可证明.
(2)由(1)可得:an+1-an=4+2(n-1)=2n+2.利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1可得an.再利用“裂项求和”方法即可得出.
解答 (1)证明:∵an+2=2an+1-an+2,
∴(an+2-an+1)-(an+1-an)=2,a2-a1=4,
∴数列{an+1-an}是等差数列,首项为4,公差为2.
(2)解:由(1)可得:an+1-an=4+2(n-1)=2n+2.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n+2(n-1)+…+2×2+2=$2×\frac{n(n+1)}{2}$=n2+n.
∴$\frac{1}{{a}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$=$(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2016}-\frac{1}{2017})$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$.
点评 本题考查了等差数列的定义通项公式及其求和公式、“累加求和”方法、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
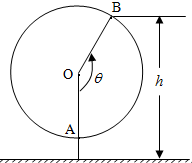 如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.
如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
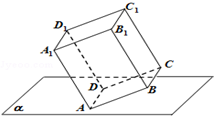 长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.
长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com