
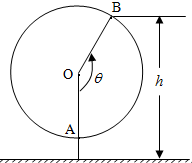
 如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.
如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.分析 (Ⅰ)以圆心O为原点,建立适当的平面直角坐标系,根据三角函数的定义写出点B的坐标,计算θ=150°时h的值即可;
(Ⅱ)根据点A在圆上转动的周期求出角速度,再写出h与t的函数解析式即可.
解答 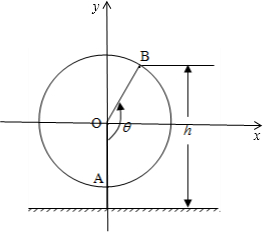 解:(Ⅰ)以圆心O为原点,
解:(Ⅰ)以圆心O为原点,
建立平面直角坐标系如图所示,
则以Ox为始边,OB为终边的角为θ-90°,
故点B的坐标为(5cos(θ-90°),5sin(θ-90°)),
∴h=6+5sin(θ-90°),
当θ=150°时,h=6+5sin(150°-90°)=6+$\frac{5\sqrt{3}}{2}$(米);
(Ⅱ)点A在圆上转动的周期是60秒,
所以角速度是$\frac{2π}{60}$=$\frac{π}{30}$,
故t秒转过的弧度数为$\frac{π}{30}$t,
所以h与t的函数解析式为
h=6+5sin($\frac{π}{30}$t-$\frac{π}{2}$),t∈[0,+∞).
点评 本题考查了在实际问题中建立三角函数模型的应用问题,在建立函数模型的过程中,以圆心O为原点,以水平方向为x轴方向,以竖直方向为Y轴方向建立平面直角坐标系,是解决本题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com