
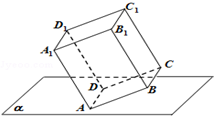
 长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.
长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$. 分析 由题意,四边形ABCD和ADD1A1的面积分别为4和6,长方体在平面α内的射影可由这两个四边形在平面α内的射影组合而成.分别求出最小与最大,即可求出长方体在平面α内的射影所构成的图形面积的取值范围.
解答 解:由题意,四边形ABCD和ADD1A1的面积分别为4和6,
长方体在平面α内的射影可由这两个四边形在平面α内的射影组合而成.显然,Smin=4.
若记平面ABCD与平面α所成角为θ,则平面ADD1A1与平面α所成角为$\frac{π}{2}$-θ.
它们在平面α内的射影分别为4cosθ和6cos($\frac{π}{2}$-θ)=6sinθ,
所以,S=4cosθ+6sinθ=2$\sqrt{13}$sin(θ+φ)(其中,tanφ=$\frac{2}{3}$),
因此,Smax=2$\sqrt{13}$,当且仅当θ=$\frac{π}{2}$-φ时取到.
因此$4≤S≤2\sqrt{13}$.
故答案为:$4≤S≤2\sqrt{13}$.
点评 本题考查长方体在平面α内的射影所构成的图形面积的取值范围,考查三角函数知识,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\sqrt{x}$)2 | B. | y=$\sqrt{{x}^{2}}$ | C. | y=$\left\{\begin{array}{l}{x,(x>0)}\\{-x,(x<0)}\end{array}\right.$ | D. | y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
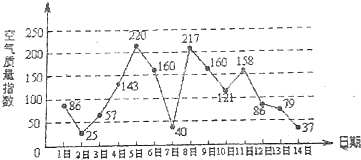 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{1024}$ | D. | $\frac{1}{256}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com