
���� ��1���������������һ���²�Ʒ�з��ɹ�Ϊ�¼�A����������϶࣬����Ҫ����¼��ĸ��ʣ�������������¼�����û��һ���²�Ʒ�з��ɹ������ݶ�������ͬʱ�����ĸ��ʼ��㷽��������Ķ����¼��ĸ��ʣ������û�Ϊ�����¼�����֮��Ĺ�ϵ������Ϊ1�����������Ӧ�ĸ��ʣ�
��2���������⣬�з��²�Ʒ�Ľ����Ϊ������������ö�������ͬʱ�����ĸ��ʼ��㷽���ֱ�õ�ÿ������ĸ��ʣ��ٸ������������ʱ�������ɵõ���������ķֲ��У������ø������Ӧ������ɼ�֮�ͼ��ɵõ���ѧ������
��� �⣺��1����E={�����з��²�Ʒ�ɹ�}��F={�����з��²�Ʒ�ɹ�}��
������֪P��E��=$\frac{3}{4}$��P��$\overline{E}$��=$\frac{1}{4}$��P��F��=$\frac{2}{3}$��P��$\overline{F}$��=$\frac{1}{3}$��
���¼�E��F��E��$\overline{F}$��$\overline{E}$ ��F��$\overline{E}$��$\overline{F}$���������
��H={������һ���²�Ʒ�з��ɹ�}����$\overline{H}$=$\overline{E}$$\overline{E}\overline{F}$��
��P��$\overline{H}$��=P��$\overrightarrow{E}$$\overline{E}\overline{F}$��=P��$\overline{E}$��P��$\overline{E}$��P��$\overline{F}$��=$\frac{1}{4}$��$\frac{1}{4}��\frac{1}{3}$=$\frac{1}{48}$��
�ʸ���ҵ�����������һ���²�Ʒ�з��ɹ��ĸ���Ϊ��
P��H��=1-P��$\overline{H}$��=1-$\frac{1}{48}$=$\frac{47}{48}$��
��2������ҵ�ɻ�����ΪX ������Ԫ������X�Ŀ���ȡֵΪ-30��30��90��150��
��P��X=-30��=P��$\overline{E}$$\overline{E}\overline{F}$��=$\frac{1}{4}$��$\frac{1}{4}��\frac{1}{3}=\frac{1}{48}$��
P��X=30��=P��E$\overline{E}\overline{F}$��+P��$\overline{E}E\overline{F}$��+P��$\overline{E}\overline{E}F$��=$\frac{3}{4}��\frac{1}{4}��\frac{1}{3}$+$\frac{1}{4}��\frac{3}{4}��\frac{1}{3}$+$\frac{1}{4}��\frac{1}{4}��\frac{2}{3}$=$\frac{1}{6}$��
P��X=90��=P��$\overline{E}EF$��+P��E$\overline{E}F$��+P��EE$\overline{F}$��=$\frac{1}{4}��\frac{3}{4}��\frac{2}{3}+\frac{3}{4}��\frac{1}{4}��\frac{2}{3}$+$\frac{3}{4}��\frac{3}{4}��\frac{1}{3}$=$\frac{7}{16}$��
P��X=150��=P��EEF��=$\frac{3}{4}��\frac{3}{4}��\frac{2}{3}$=$\frac{3}{8}$��
�����ҵ���������3���²�Ʒ�ϻ�õ�����X�ķֲ���Ϊ��
| X | -30 | 30 | 90 | 150 |
| P | $\frac{1}{48}$ | $\frac{1}{6}$ | $\frac{7}{16}$ | $\frac{3}{8}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�


 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
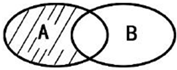 ��֪����ʽ|x-2|��3�Ľ⼯Ϊ A������y=ln��1-x���Ķ�����ΪB����ͼ����Ӱ���ֱ�ʾ�ļ���Ϊ{x|1��x��5}��
��֪����ʽ|x-2|��3�Ľ⼯Ϊ A������y=ln��1-x���Ķ�����ΪB����ͼ����Ӱ���ֱ�ʾ�ļ���Ϊ{x|1��x��5}���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
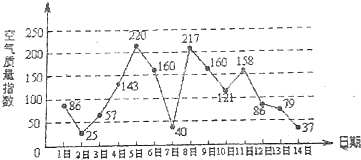 ��ͼ��ij��3��1����14�յĿ�������ָ������ͼ����������ָ��С��100��ʾ����������������������ָ������200��ʾ�����ض���Ⱦ��ij�����ѡ��3��1����3��13���е�ijһ�쵽����У���ͣ��2�죮
��ͼ��ij��3��1����14�յĿ�������ָ������ͼ����������ָ��С��100��ʾ����������������������ָ������200��ʾ�����ض���Ⱦ��ij�����ѡ��3��1����3��13���е�ijһ�쵽����У���ͣ��2�죮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
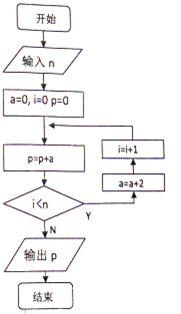 ִ����ͼ��ʾ�ij����ͼ����������n��6����ô�����p�ǣ�������
ִ����ͼ��ʾ�ij����ͼ����������n��6����ô�����p�ǣ�������| A�� | 12 | B�� | 42 | C�� | 30 | D�� | 40 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-1��2+y2=4 | B�� | ��x-2��2+y2=4 | C�� | ��x+1��2+y2=4 | D�� | ��x+2��2+y2=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com