
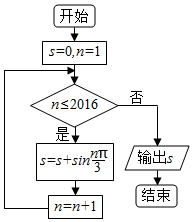
分析 根据题中的流程图,模拟运行,依次根据条件计算s和n的值,直到n>2016运行结束,输出此时的s的值即为答案.
解答 解:根据题中的流程图,模拟运行如下:
输入s=0,n=1,此时n≤2013,符合条件,
∴s=0+sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,n=2,此时n≤2013,符合条件,
∴s=$\frac{\sqrt{3}}{2}$+sin$\frac{2π}{3}$=$\sqrt{3}$,n=3,此时n≤2013,符合条件,
∴s=$\sqrt{3}$+sinπ=$\sqrt{3}$,n=4,此时n≤2013,符合条件,
∴s=$\sqrt{3}$+sin$\frac{4π}{3}$=$\frac{\sqrt{3}}{2}$,n=5,此时n≤2013,符合条件,
∴s=$\frac{\sqrt{3}}{2}$+sin$\frac{5π}{3}$=0,n=6,此时n≤2013,符合条件,
∴s=0+sin2π=0,n=7,此时n≤2013,符合条件,
∴s=0+sin$\frac{7π}{3}$=$\frac{\sqrt{3}}{2}$,n=8,此时n≤2013,符合条件,
…
通过运行即可发现运行中的s的值具有周期性,周期为6,2016=6×336,
∴s=0,n=2017,此时n>2016,不符合条件,
结束运行,输出s=0.
故答案为:0.
点评 本题考查了程序框图.根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,要按照流程图中的运行顺序进行求解是关键.属于基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
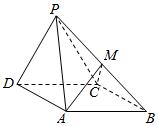 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,面PCD⊥面ABCD,PC=PD=CD=2,点M为线段PB上异于P、B的点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,面PCD⊥面ABCD,PC=PD=CD=2,点M为线段PB上异于P、B的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)
已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
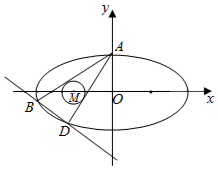 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点为A(0,1),离心率为$\frac{{\sqrt{3}}}{2}$.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的上顶点为A(0,1),离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤4} | B. | {x|x≥1} | C. | {x|1≤x≤4} | D. | {x|x≥-2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com