
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
分析 由题意,利用周期公式可求$ω=\frac{1}{2}$.由f(x)≤f($\frac{π}{3}$)恒成立,结合范围|φ|<$\frac{π}{2}$,可求φ=$\frac{π}{3}$,令$\frac{1}{2}x+\frac{π}{3}$=kπ(k∈Z),即可解得f(x)的对称中心,即可得解.
解答 解:由f(x)=sin(ωx+φ)的最小正周期为4π,得$ω=\frac{1}{2}$.
因为f(x)≤f($\frac{π}{3}$)恒成立,
所以f(x)${\;}_{max}=f(\frac{π}{3})$,即$\frac{1}{2}×\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ(k∈Z),
由|φ|<$\frac{π}{2}$,得φ=$\frac{π}{3}$,
故f(x)=sin($\frac{1}{2}x+\frac{π}{3}$).
令$\frac{1}{2}x+\frac{π}{3}$=kπ(k∈Z),得x=2kπ-$\frac{2π}{3}$,(k∈Z),
故f(x)的对称中心为(2kπ-$\frac{2π}{3}$,0)(k∈Z),
当k=0时,f(x)的对称中心为(-$\frac{2π}{3}$,0),
故选:A.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质的应用,考查了数形结合思想的应用,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
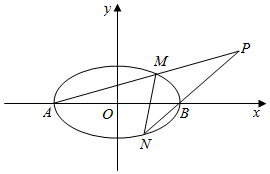 已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).
已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{10}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
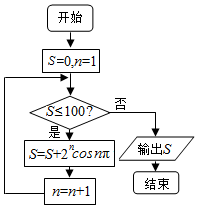
| A. | $\frac{{{2^{99}}-2}}{3}$ | B. | $\frac{{{2^{100}}-2}}{3}$ | C. | $\frac{{{2^{101}}-2}}{3}$ | D. | $\frac{{{2^{102}}-2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∨q | C. | p∨q | D. | ¬p∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com