
分析 $|{1-\frac{x-1}{3}}|$<2?-2<x<10,记A={x|-2<x<10},B={x|x2-2x+1-m2<0},由?p是?q的充分非必要条件,可知:B?A.再利用二次函数的图象与性质即可得出.
解答 解:$|{1-\frac{x-1}{3}}|$<2?-2<x<10,…(2分)
记A={x|-2<x<10},
B={x|x2-2x+1-m2<0},
由?p是?q的充分非必要条件,可知:B?A…(4分)
记,f(x)=x2-2x+1-m2,则$\left\{\begin{array}{l}f(-2)≥0\\ f(10)≥0.\end{array}\right.$,即$\left\{\begin{array}{l}9-{m^2}≥0\\ 81-{m^2}≥0.\end{array}\right.$
解此不等式组得,-3≤m≤3…(8分)
经检验m=±3时上等式组中两不等式的等号不同时成立.
∴m的取值范围是-3≤m≤3…(10分)
点评 本题考查了不等式的解法、简易逻辑的判定方法、二次函数的图象与性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
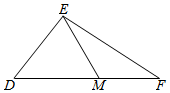 如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.
如图所示,在△DEF中,M是在线段DF上,DE=3,DM=EM=2,sin∠F=$\frac{3}{5}$=,则边EF的长为$\frac{5\sqrt{7}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
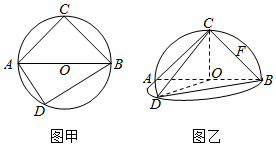 如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:
如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com