Question

【题目】已知函数(且)，

（1）若，且函数的值域为，求的解析式；

（2）在（1）的条件下，当时，时单调函数，求实数的取值范围；

（3）当，时，若对于任意，不等式恒成立，求实数的取值范围

Answer 1

【答案】（1）；（2）或；（3）.

【解析】

（1）由函数的值域为，得，再结合，从而求得的值，进而求得函数的解析式；

（2）函数的对称轴不在区间内即可；

（3）将不等式恒成立转化为不等式组对于任意，恒成立，看成以为主元，再分别研究两个不等式恒成立问题.

（1）函数的值域为，所以，

又，所以，解得：

所以.

（2）因为，

对称轴为，

所以或，解得：或.

（3）当时，，

因为，

所以不等式组对于任意，恒成立.

所以不等式组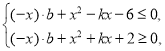对于任意，恒成立.

所以对于任意恒成立.

先考虑不等式对于任意恒成立，所以；

再考虑不等式对于任意恒成立（此时只考虑情况），

因为函数的对称轴为，

①当时，不等式对于任意恒成立；

②当时，，则，

所以；

综上所述：.