Question

7．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，且它的左焦点F₁与右顶点A的距离|AF₁|=6．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过点T（-3，0）作与x轴不重合的直线l交椭圆于P，Q两点，连接AP，AQ分别交直线x=-$\frac{16}{3}$于R，S两点，求证：直线RT与直线ST的斜率之积为定值．

Answer 1

分析 （Ⅰ）设椭圆的左焦点F₁的坐标为（-c，0），由离心率公式和椭圆a，b，c的关系，即可求得a，b，c，进而得到椭圆方程；
（Ⅱ）设P（x₁，y₁），Q（x₂，y₂），直线PQ的方程，联立椭圆方程，运用韦达定理，以及三点共线求得R，S的纵坐标，再由直线的斜率公式，即可计算直线RT与直线ST的斜率之积为一定值．

解答 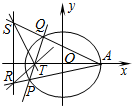（Ⅰ）解：设椭圆的左焦点F₁的坐标为（-c，0），
依题意b²=a²-c²，$e=\frac{c}{a}=\frac{1}{2}$，|AF₁|=a+c=6．
解得a=4，c=2，b²=a²-c²=12．
∴椭圆C的标准方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$．
（Ⅱ）证明：设P（x₁，y₁），Q（x₂，y₂），
由直线PQ与x轴不重合，故可设直线PQ：y=k（x+3），
由$\left\{{\begin{array}{l}{y=k（x+3）}\\{\frac{x^2}{16}+\frac{y^2}{12}=1}\end{array}}\right.$整理得（4k²+3）x²+24k²x+（36k²-48）=0．
则${x_1}+{x_2}=-\frac{{24{k^2}}}{{4{k^2}+3}}$，${x_1}{x_2}=\frac{{36{k^2}-48}}{{4{k^2}+3}}$．
由A，P，R三点共线，可得$\frac{{{y_R}-0}}{{-\frac{16}{3}-4}}=\frac{{{y_1}-0}}{{{x_1}-4}}$，即${y_R}=-\frac{28}{3}•\frac{y_1}{{{x_1}-4}}$，
由A，Q，S三点共线，同理可得${y_S}=-\frac{28}{3}•\frac{y_2}{{{x_2}-4}}$．${k_{RT}}•{k_{ST}}=\frac{{{y_R}-0}}{{-\frac{16}{3}+3}}•\frac{{{y_S}-0}}{{-\frac{16}{3}+3}}=\frac{{9{y_R}•{y_S}}}{49}=\frac{{16{y_1}{y_2}}}{{{x_1}{x_2}-4（{x_1}+{x_2}）+16}}$．
而y₁y₂=${k^2}（{x_1}+3）（{x_2}+3）={k^2}[{x_1}{x_2}+3（{x_1}+{x_2}）+9]$，
故${k_{RT}}•{k_{ST}}=16{k^2}•\frac{{{x_1}{x_2}+3（{x_1}+{x_2}）+9}}{{{x_1}{x_2}-4（{x_1}+{x_2}）+16}}$
=$16{k^2}•\frac{{\frac{{36{k^2}-48}}{{4{k^2}+3}}-\frac{{72{k^2}}}{{4{k^2}+3}}+\frac{{36{k^2}+27}}{{4{k^2}+3}}}}{{\frac{{36{k^2}-48}}{{4{k^2}+3}}+\frac{{96{k^2}}}{{4{k^2}+3}}+\frac{{64{k^2}+48}}{{4{k^2}+3}}}}=-\frac{12}{7}$．
∴直线RT与直线ST的斜率之积为定值$-\frac{12}{7}$．

点评 本题考查椭圆的方程和性质，主要考查离心率的运用，同时考查直线和椭圆方程联立，运用韦达定理，以及直线的斜率公式的运用，具有一定的运算量，属于中档题和易错题．