Question

【题目】在平面直角坐标系xOy中，曲线C的参数方程为 （α为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为 ．
（1）求C的普通方程和l的倾斜角；
（2）设点P（0，2），l和C交于A，B两点，求|PA|+|PB|．

Answer 1

【答案】
（1）解法一：由 消去参数α，得 ，

即C的普通方程为 ．

由 ，得ρsinθ﹣ρcosθ=2，…（*）

将 代入（*），化简得y=x+2，

所以直线l的倾斜角为 ．

解法二：同解法一．

（2）解法一：由（1）知，点P（0，2）在直线l上，可设直线l的参数方程为 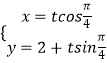（t为参数），

即 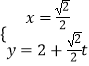（t为参数），

代入 并化简，得 ．

．

设A，B两点对应的参数分别为t1，t2，

则 ，所以t1＜0，t2＜0，）

所以 ．

解法二：直线l的普通方程为y=x+2．

由 消去y得10x2+36x+27=0，

于是△=362﹣4×10×27=216＞0．

设A（x1，y1），B（x2，y2），则 ， ，所以x1＜0，x2＜0，

故

【解析】解法一：（1）由参数方程消去参数α，得椭圆的普通方程，由极坐标方程，通过两角和与差的三角函数转化求解出普通方程即可求出直线l的倾斜角．（2）设出直线l的参数方程，代入椭圆方程并化简，设A，B两点对应的参数分别为t1 ， t2 ， 利用参数的几何意义求解即可．解法二：（1）同解法一．（2）利用直线l的普通方程与椭圆的方程联立，设A（x1 ， y1），B（x2 ， y2），利用韦达定理以及弦长公式求解即可．