
分析 (I)利用等差数列的通项公式可得an.由于数列{bn}为等比数列.已知a1b1+a2b2+a3b3+…+anbn=(n-1)•3n+1+3.分别令n=1,2,再利用等比数列的通项公式即可得出.
(Ⅱ)由于(an+1)•log3bn+2•cn=2n(n+2)•cn=1,可得cn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),再利用“裂项求和”方法即可得出.
解答 解:(Ⅰ)∵an+1=an+2,n∈N*,a1=1,
∴{an}是1为首项,2为公差的等差数列.
∴an=2n-1. …(3分)
∵a1b1+a2b2+a3b3+…+anbn=(n-1)•3n+1+3,
∴a1b1=3,a1b1+a2b2=30,
解得b1=3,b2=9.
∴{bn}的通项公式为bn=3n. …(7分)
(Ⅱ)∴an•(1+2log3bn)•cn=(2n-1)•(2n+1)•cn=1,
∴cn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$) …(10分)
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{2n-3}$-$\frac{1}{2n-1}$)+$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$. …(13分)
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法、对数的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c都是奇数 | |
| B. | a、b、c都是偶数 | |
| C. | a、b、c中至少有两个奇数 | |
| D. | a、b、c中至少有两个奇数或都是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
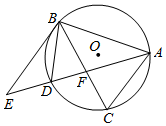 如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.
如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com