
分析 (1)直接利用$\sqrt{2x+1}$≥0求得原函数的值域;
(2)把已知函数解析式变形,然后分离常数,即可求得函数的值域.
解答 解:(1)∵$\sqrt{2x+1}≥0$,∴y=$\sqrt{2x+1}$+1≥1,则函数y=$\sqrt{2x+1}$+1的值域为[1,+∞);
(2)y=$\frac{1-{x}^{2}}{1+{x}^{2}}$=$-\frac{{x}^{2}+1-2}{{x}^{2}+1}=-1+\frac{2}{{x}^{2}+1}$,
∵x2+1≥1,∴$0<\frac{1}{{x}^{2}+1}≤1$,则0<$\frac{2}{{x}^{2}+1}≤2$,
∴-1$<-1+\frac{2}{{x}^{2}+1}≤1$,
故y=$\frac{1-{x}^{2}}{1+{x}^{2}}$的值域为(-1,1].
点评 本题考查函数的值域,训练了利用函数的单调性及分离常数法求函数的值域,是基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
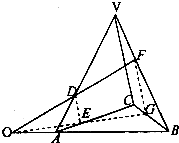 在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且$\frac{AD}{AV}$=$\frac{AE}{AC}$=$\frac{VF}{VB}$=$\frac{CG}{CB}$=$\frac{1}{3}$.求证:直线DF、EG、AB共点.
在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且$\frac{AD}{AV}$=$\frac{AE}{AC}$=$\frac{VF}{VB}$=$\frac{CG}{CB}$=$\frac{1}{3}$.求证:直线DF、EG、AB共点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com