
分析 由f(x)≥g(x)求得x的范围,写出分段函数,分段求出值域,取并集得答案.
解答 解:由f(x)≥g(x),得1-2x2≥x2-2x,解得$-\frac{1}{3}≤x≤1$,
∴$F(x)=\left\{\begin{array}{l}{{x}^{2}-2x,-\frac{1}{3}≤x≤1}\\{1-2{x}^{2},x<-\frac{1}{3}或x>1}\end{array}\right.$,
当F(x)=x2-2x(-$\frac{1}{3}≤x≤1$)时,F(x)∈[-1,$\frac{7}{9}$];
当F(x)=1-2x2(x$<-\frac{1}{3}$或x>1)时,F(x)∈(-∞,$\frac{7}{9}$).
取并集得F(x)∈(-∞,$\frac{7}{9}$].
点评 本题考查函数的值域,注意防盗函数的值域分段求,最后取并集,是基础题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
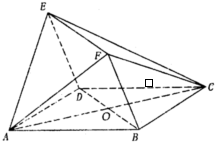 如图所示,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图所示,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com