
���� ��c��a��b������λ��������з��������ɵó����ۣ�
��� 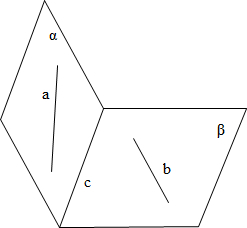 �⣺��a?����c?����b?�£�c?�£�
�⣺��a?����c?����b?�£�c?�£�
��a��c���棬b��c���棬
��1����c��a��b�����ཻ����c��a��c��b��
��a��b����a��bΪ����ֱ��ì�ܣ�
��2����a��c��b��c�ཻ�ڵ�A����b��aû�й����㣬
��a��b�Ȳ�ƽ��Ҳ���ཻ����a��bΪ����ֱ�ߣ�
��3����c��a��b���ཻ���ҽ�����ͬ����a��bΪ�ֱཻ�ߣ���a��bΪ����ֱ��ì�ܣ�
��4����c��a��b���ཻ���ҽ��㲻��ͬ����a��bû�й����㣬��a��b��ƽ�У�
��a��bΪ����ֱ�ߣ�
���ϣ���a��bΪ����ֱ��ʱ��c������a��b�е�һ���ཻ��
���˵����ȷ�����Ҷ�˵������
���� ���⿼���˿ռ�ֱ�ߵ�λ�ù�ϵ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
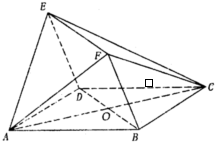 ��ͼ��ʾ���ı���ABCD��BDEF��Ϊ���Σ���DAB=��DBF=60�㣬��FA=FC��
��ͼ��ʾ���ı���ABCD��BDEF��Ϊ���Σ���DAB=��DBF=60�㣬��FA=FC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com