
| A. | 1 | B. | 4 | C. | 7 | D. | 16 |
分析 构造函数g(x)=f(x)-10x,则1,2,3为方程f(x)-10x=0的三个根,可设方程f(x)-10x=0的另一根为m,则方程f(x)-10x=(x-1)(x-2)(x-3)(x-m),由此能求出$\frac{1}{4}$[f(4)+f(0)].
解答 解:∵f(x)=x4+ax3+bx2+cx+d,其中a、b、c、d为常数.
f(1)=10,f(2)=20,f(3)=30,
∴构造函数g(x)=f(x)-10x,则g(1)=g(2)=g(3)=0,
即1,2,3为方程f(x)-10x=0的三个根
∵方程f(x)-10x=0有四个根,
故可设方程f(x)-10x=0的另一根为m
则方程f(x)-10x=(x-1)(x-2)(x-3)(x-m)
∴f(x)=(x-1)(x-2)(x-3)(x-m)+10x
故$\frac{1}{4}$[f(4)+f(0)]=$\frac{1}{4}$[(4-1)(4-2)(4-3)(4-m)+40+(0-1)(0-2)(0-3)(0-m)+0]=16.
故选:D.
点评 本题考查函数值的求法,是中档题,解题时要认真审题,注意构造法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
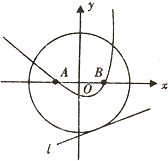 如图,⊙O:x2+y2=16,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A,B两点的抛 物线以直线l为准线,则该抛物线的焦点的轨迹是( )
如图,⊙O:x2+y2=16,A(-2,0),B(2,0)为两个定点,l是⊙O的一条切线,若过A,B两点的抛 物线以直线l为准线,则该抛物线的焦点的轨迹是( )| A. | 圆 | B. | 双曲线 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>3或-3<x<0} | B. | {x|x<3或0<x<-3} | C. | {x|x<-3或x>3} | D. | {x|-3<x<0或0<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com