
分析 (1)由f(0)=2,f($\frac{π}{3}$)=$\frac{{1+\sqrt{3}}}{2}$可得:a=1,b=2,于是可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,从而可求f(x)的最大值与最小值;
(2)由(1)得f(x)$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,即可求得其单调增区间;
(3)f(α)=f(β),可得2α+$\frac{π}{4}$=2kπ+(2β+$\frac{π}{4}$)或2α+$\frac{π}{4}$=2kπ+π-(2β+$\frac{π}{4}$),得到α+β的值,从而求得tan(α+β)的值.
解答 解:(Ⅰ)由f(0)=2,f($\frac{π}{3}$)=$\frac{{1+\sqrt{3}}}{2}$可得:a=1,b=2,
∴f(x)=2cos2x+2sinxcosx
=sin2x+cos2x+1
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,
∴当x=$\frac{π}{8}$+kπ(k∈Z)时,f(x)取得最大值,为$\sqrt{2}$+1;
当x=$\frac{5π}{8}$+kπ(k∈Z)时,f(x)取得最小值,为-$\sqrt{2}$+1;
(Ⅱ)令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
则-$\frac{3π}{8}$+kπ≤x≤$\frac{π}{8}$+kπ,k∈Z,
∴f(x)的单调增区间为[-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ],k∈Z.
(3)∵f(α)=f(β),∴sin(2α+$\frac{π}{4}$)=sin(2β+$\frac{π}{4}$).
∴2α+$\frac{π}{4}$=2kπ+(2β+$\frac{π}{4}$)或2α+$\frac{π}{4}$=2kπ+π-(2β+$\frac{π}{4}$),
∴α-β=kπ(舍去)或α+β=kπ+$\frac{π}{4}$,k∈Z,∴tan(α+β)=tan(kπ+$\frac{π}{4}$)=1,
即:tan(α+β)=1.
点评 本题考查三角函数的化简求值,考查正弦函数的单调性与最值,突出辅助角公式的应用,考查分析与应用能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 7 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
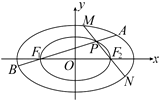 如图,已知点F1,F2是椭圆C1:$\frac{x^2}{4}$+$\frac{y^2}{2}$=1的左、右焦点,点P是椭圆C2:$\frac{x^2}{2}$+y2=1上异于其长轴端点的任意动点,直线PF1,PF2与椭圆C1的交点分别是A,B和M,N,记直线AB,MN的斜率分别为k1,k2.
如图,已知点F1,F2是椭圆C1:$\frac{x^2}{4}$+$\frac{y^2}{2}$=1的左、右焦点,点P是椭圆C2:$\frac{x^2}{2}$+y2=1上异于其长轴端点的任意动点,直线PF1,PF2与椭圆C1的交点分别是A,B和M,N,记直线AB,MN的斜率分别为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
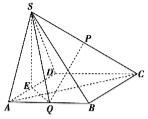 如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com