
分析 (1)数列{an}满足:a1=2,$n{a_{n+1}}=(n+1){a_n}+n(n+1),n∈{N^*}$,变形为$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,利用等差数列的通项公式即可得出.
(2)数列{bn}满足:对一切n∈N*,均有${b_1}{b_2}…{b_n}={(\sqrt{2})^{a_n}}$.可得b1=2.当n≥2时,bn=$\frac{(\sqrt{2})^{{a}_{n}}}{(\sqrt{2})^{{a}_{n-1}}}$=2n.利用等比数列的前n项和公式可得Sn.
(3)由cn=$\frac{1}{{b}_{n}}$-$\frac{1}{{a}_{n}}$=$(\frac{1}{2})^{n}$-$(\frac{1}{n}-\frac{1}{n+1})$.利用等比数列的前n项和公式、“裂项求和”方法可得数列{cn}的前n项和为Tn.再利用其单调性即可得出.
解答 (1)证明:数列{an}满足:a1=2,$n{a_{n+1}}=(n+1){a_n}+n(n+1),n∈{N^*}$,
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,
∴数列$\{\frac{a_n}{n}\}$为等差数列,公差为1,首项为2.
∴$\frac{{a}_{n}}{n}$=2+(n-1)=n+1,∴an=n(n+1).
(2)解:数列{bn}满足:对一切n∈N*,均有${b_1}{b_2}…{b_n}={(\sqrt{2})^{a_n}}$.
∴b1=$(\sqrt{2})^{2}$=2.
当n≥2时,bn=$\frac{(\sqrt{2})^{{a}_{n}}}{(\sqrt{2})^{{a}_{n-1}}}$=$(\sqrt{2})^{{a}_{n}-{a}_{n-1}}$=$(\sqrt{2})^{2n}$=2n.(n=1时也成立).
∴数列{bn}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.
(3)解:${c_n}=\frac{{{a_n}-{b_n}}}{{{a_n}{b_n}}}(n∈{N^*})$,
cn=$\frac{{a}_{n}-{b}_{n}}{{a}_{n}{b}_{n}}$=$\frac{1}{{b}_{n}}$-$\frac{1}{{a}_{n}}$=$(\frac{1}{2})^{n}$-$(\frac{1}{n}-\frac{1}{n+1})$.
∴数列{cn}的前n项和为Tn=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$(1-\frac{1}{n+1})$=$\frac{1}{n+1}$-$\frac{1}{{2}^{n}}$.
Tn+1-Tn=$(\frac{1}{n+2}-\frac{1}{{2}^{n+1}})$-$(\frac{1}{n+1}-\frac{1}{{2}^{n}})$=$\frac{1}{{2}^{n+1}}$-$\frac{1}{(n+1)(n+2)}$
=$\frac{(n+1)(n+2)-{2}^{n+1}}{(n+1)(n+2)•{2}^{n+1}}$,
可知:n=1,2,3时,Tn+1>Tn;
n≥4时,Tn+1<Tn.
∴T1<T2<T3<T4>T5>T6…,
∴T4为最大值.
∴取正整数k=4,使得对任意n∈N*,均有T4≥Tn.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法、数列的单调性,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥n,则n∥α | D. | m⊥α,m∥n,则n⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
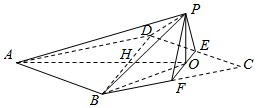 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4}^{n}-1}{3}$ | B. | $\frac{({2}^{n}-1)^{2}}{3}$ | C. | 4n-1 | D. | (2n-1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [${4}^{\frac{1}{3}}$,+∞) | B. | [${4}^{\frac{1}{3}}$,6] | C. | [4,+∞) | D. | [3,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com