
分析 (1)根据导数的公式进行求解即可.
(2)根据数学归纳法进行证明即可.
解答 解:(1)${f_1}(x)={f_0}^/(x)=sinx+xcosx$,
${f_2}(x)={f_1}^/(x)=cosx+cosx-xsinx=2cosx-xsinx$,
${f_3}(x)={f_{21}}^/(x)=-2sinx-sinx-xcosx=-3sinx-xcosx$,
(2)归纳:${f_1}(x)=sinx+xcosx=1×sin(x+\frac{1-1}{2}π)+xcos(x+\frac{1-1}{2}π)$,
${f_2}(x)=2cosx-xsinx=2×sin(x+\frac{2-1}{2}π)+xcos(x+\frac{2-1}{2}π)$,
${f_3}(x)=-3sinx-xcosx=3×sin(x+\frac{3-1}{2}π)+xcos(x+\frac{3-1}{2}π)$
猜想:${f_n}(x)=nsin(x+\frac{n-1}{2}π)+xcos(x+\frac{n-1}{2}π)$,n∈N*
证明:①当n=1时,f1(x)=sinx+xcosx,结论成立;
②假设n=k(k∈N*)时,结论成立,
即${f_k}(x)=ksin(x+\frac{k-1}{2}π)+xcos(x+\frac{k-1}{2}π)$,
当n=k+1时,${f_{k+1}}(x)={f_k}^/(x)=kcos(x+\frac{k-1}{2}π)+cos(x+\frac{k-1}{2}π)-xsin(x+\frac{k-1}{2}π)$=$(k+1)cos(x+\frac{k-1}{2}π)-xsin(x+\frac{k-1}{2}π)$=$(k+1)sin(x+\frac{k-1}{2}π+\frac{π}{2})$+$xcos(x+\frac{k-1}{2}π+\frac{π}{2})$
=$(k+1)sin[{x+\frac{(k+1)-1}{2}π}]$+$xcos[{x+\frac{(k+1)-1}{2}π}]$
所以当n=k+1时,结论也成立
由①②可知,当n∈N*时,${f_n}(x)=nsin(x+\frac{n-1}{2}π)+xcos(x+\frac{n-1}{2}π)$.
点评 本题主要考查导数的运算,以及数学归纳法的证明和应用,考查学生的运算和推理能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x+3y-7=0 | B. | 3x+4y-7=0 | C. | 3x-4y+1=0 | D. | 4x-3y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
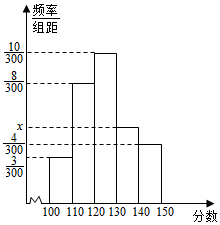 我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.
我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com