
分析 (1)利用椭圆的定义判断点E的轨迹是以A、C为焦点的椭圆,求出a、b的值,即得椭圆的方程;
(2)设AM与CN的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AM|、|CN|,根据已知条件|AM|-|CN|=$\frac{3\sqrt{2}}{8}$求得m值,则直线AM的方程可求.
解答 解:(1)由题意得,圆心C(1,0),半径等于2$\sqrt{2}$,|EA|=|EB|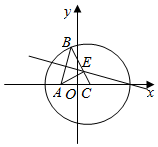
∴|EC|+|EA|=|EC|+|EB|=|CB|=2$\sqrt{2}$>|AC|,
故点E的轨迹是以A、C为焦点的椭圆,
∵2a=2$\sqrt{2}$,c=1,
∴$a=\sqrt{2}$,c=1,则b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2))∵椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$,A(-1,0),C(1,0),
又∵直线AM∥CN,
∴设AM与CN的方程分别为x+1=my,x-1=my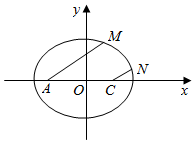
设M(x1,y1),N(x2,y2),y1>0,y2>0,
∴由$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{2}+{{y}_{1}}^{2}=1}\\{{x}_{1}+1=m{y}_{1}}\end{array}\right.$,得(m2+2)${{y}_{1}}^{2}$-2my1-1=0.
∴${y}_{1}=\frac{m+\sqrt{2{m}^{2}+2}}{{m}^{2}+2}$,
∴|AM|=$\sqrt{{m}^{2}+1}•|0-{y}_{1}|$=$\frac{\sqrt{2}({m}^{2}+1)+m\sqrt{{m}^{2}+1}}{{m}^{2}+2}$,①
同理|CN|=$\frac{\sqrt{2}({m}^{2}+1)-m\sqrt{{m}^{2}+1}}{{m}^{2}+2}$,②
∵|AM|-|CN|=$\frac{3\sqrt{2}}{8}$,
∴由①②得|AM|-|CN|=$\frac{2m\sqrt{{m}^{2}+1}}{{m}^{2}+2}$=$\frac{3\sqrt{2}}{8}$,解得m2=$\frac{39}{119}$.
由题意可得m>0,∴m=$\frac{39\sqrt{119}}{119}$.
∴直线AM的方程为x-$\frac{39\sqrt{119}}{119}y+1=0$.
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,解题时要注意等价转化思想的合理运用,是中档题.


科目:高中数学 来源: 题型:解答题
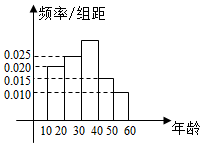 第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.
第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com