
分析 (1)由题意,先求出从两个盒子内各取两球的所有取法,用分步原理求解,再求出全是红球的取法,根据概率公式计算即可;
(2)求出全是黑球的取法的概率,由公式求概率即可.
解答 解:(1)设“从甲坛子内取出的2个球均为红球”为事件A,“从乙坛子内取出的2个球均为红球”为事件B.
由于事件A,B相互独立,所以取出的4个球均为红球的概率为P(A•B)=P(A)P(B)=$\frac{1}{{C}_{4}^{2}}$•$\frac{1}{{C}_{4}^{2}}$=$\frac{1}{36}$,
(2)设“从甲坛子内取出的2个球均为白球”为事件C,“从乙坛子内取出的2个球均为白球球”为事件D,
∴P(A)=P(B)=P(C)=P(D)=$\frac{1}{6}$,
∴取出的4个球既含有白球又含有红球的概率P=1-P(A•B)-P(C,D)=1-$\frac{1}{36}$-$\frac{1}{36}$=$\frac{17}{18}$
点评 本题考查等可能事件的概率,解题的关键是理解题中所给的事件类型及概率求法,属中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
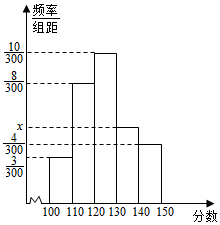 我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.
我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | 9 | C. | -9 | D. | ±9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com