
分析 运用分析法证明.由a>b>0,要证原不等式成立,可通过移项,通分,去分母,化简可得a>b,即可得证.
解答 证明:运用分析法证明.
由a>b>0,要证$\frac{a-b}{a+b}$+$\frac{2{b}^{2}}{{a}^{2}+{b}^{2}}$<1,
只要证$\frac{a-b}{a+b}$<1-$\frac{2{b}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$,
即证(a-b)(a2+b2)<(a+b)(a2-b2),
即为a3+ab2-ba2-b3<a3-ab2+ba2-b3,
即有2ab2<2ba2,即b<a,显然成立.
则有$\frac{a-b}{a+b}$+$\frac{2{b}^{2}}{{a}^{2}+{b}^{2}}$<1成立.
点评 本题考查不等式的证明,注意运用分析法证明,考查化简整理的运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
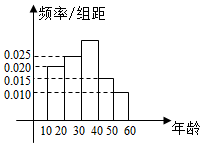 第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.
第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com