
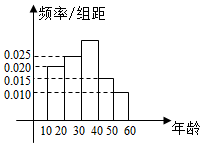
 第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.
第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.分析 (Ⅰ)由频率分布直方图,先求出年龄在[30,40)内的频率,由此能求出抽取的年龄在[30,40)内的居民人数.
(Ⅱ)依题意年龄在[10,20)、[50,60)分别抽取4人和2人,记年龄在[10,20)内的人为A,B,C,D,年龄在[50,60)内的人为1,2,进行测试的居民中至少有1人的年龄在[50,60]内的概率.
解答 解:(Ⅰ)由频率分布直方图,得:
年龄在[30,40)内的频率P=1-(0.02+0.025+0.015+0.01)×10=0.3,
故所求居民人数为300×0.3=90.
(Ⅱ)依题意年龄在[10,20)、[50,60)分别抽取4人和2人,
记年龄在[10,20)内的人为A,B,C,D,
年龄在[50,60)内的人为1,2,
故抽取2人进行测试,所有的情况为:
(A,B),(A,C),(A,D),(A,1),(A,2),(B,C),(B,D),(B,1),(B,2),
(C,D),(C,1),(C,2),(D,1),(D,2),(1,2),共15种,
∴进行测试的居民中至少有1人的年龄在[50,60]内包含的基本事件的情况有:(A,1),(A,2),(B,1),(B,2),
(C,1),(C,2),(D,1),(D,2),(1,2),共9种,
进行测试的居民中至少有1人的年龄在[50,60]内的概率p=$\frac{m}{n}$=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com