
分析 (Ⅰ)根据题意,An是线段An-2An-1的中点,可得xn与xn-1、xn-2之间的关系式,并令n=1,2,3求出答案即可.
(Ⅱ)根据(Ⅰ)的计算结果,猜想的通{an}项公式,用数学归纳法的证明步骤直接证明即可.
解答 解:(Ⅰ)${x_n}=\frac{{{x_{n-1}}+{x_{n-2}}}}{2}(n≥3)$…(2分)${a_1}=1,{a_2}=-\frac{1}{2},{a_3}=\frac{1}{4}$.…(5分)
(Ⅱ)猜想${a_n}={(-\frac{1}{2})^{n-1}}$…(6分)
证明:①当n=1时,a1=$(-\frac{1}{2})^{1-1}$=1
∴当n=1时,${a_n}={(-\frac{1}{2})^{n-1}}$成立.…(7分)
②假设当n=k时${a_k}={(-\frac{1}{2})^{k-1}}$成立.
则当n=k+1时,${a_{k+1}}={x_{k+2}}-{x_{k+1}}=\frac{{{x_{k+1}}+{x_k}}}{2}-{x_{k+1}}=-\frac{1}{2}({x_{k+1}}-{x_k})=-\frac{1}{2}{a_k}$=$-\frac{1}{2}•{(-\frac{1}{2})^{k-1}}={(-\frac{1}{2})^k}={(-\frac{1}{2})^{(k+1)-1}}$,
∴当n=k+1时,公式成立.…(11分)
综上①②得,对任意n∈N*,公式${a_n}={(-\frac{1}{2})^{n-1}}$成立.…(12分)
点评 本题考查数列递推关系式以及通项公式的应用,数学归纳法的证明方法的应用,考查计算能力与逻辑推理能力.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
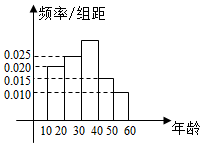 第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.
第47届联合国大会于1993年1月18日通过193号决议,确定自1993年起,每年的3月22日为“世界水日”,依次推动对水资源进行进行综合性统筹规划和管理,加强水资源保护,解决日益严重的水问题.某研究机构为了了解各年龄层的居民对“世界水日”的了解程度,随机抽取了300名年龄在[10,60]的公民进行调查,所得结果统计为如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com