
分析 利用根式与数指数幂的互化公式及根式的性质直接求解.
解答 解:(1)a•$\sqrt{-\frac{1}{a}}$=$a•\sqrt{-\frac{a}{{a}^{2}}}$=-$\sqrt{-a}$;
(2)$\sqrt{-{a}^{3}{b}^{2}}$=-a|b|$\sqrt{-a}$;
(3)∵x<0,∴$\sqrt{\frac{{y}^{3}}{12{x}^{3}}}$=$\sqrt{\frac{{y}^{2}•y}{12{x}^{2}x}}$=-$\frac{y\sqrt{3xy}}{6{x}^{2}}$;
(4)$\sqrt{(a-3)^{2}}$+$\sqrt{(a+4)^{2}}$=|a-3|+|a+4|=$\left\{\begin{array}{l}{2a+1,a≥3}\\{7,-4≤a<3}\\{-2a-1,a<-4}\end{array}\right.$.
点评 本题考查根的化简,是基础题,解题时要认真审题,注意根式与数指数幂的互化公式及根式的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱台的侧面一定不会是平行四边形 | |
| B. | 棱锥的侧面只能是三角形 | |
| C. | 由四个面围成的封闭图形只能是三棱锥 | |
| D. | 棱锥被平面截成的两部分不可能都是棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
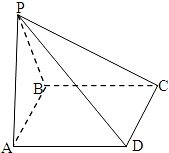 如图,在四棱锥P-ABCD中,面PAB⊥面ABCD,PA=PB=$\sqrt{3}$,且四边形ABCD为菱形,AD=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,面PAB⊥面ABCD,PA=PB=$\sqrt{3}$,且四边形ABCD为菱形,AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {4} | C. | {2,4} | D. | {2,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com