
分析 若P真,由题知:对任意x>-1,$\frac{{x}^{2}}{x+1}$=$\frac{(x+1)^{2}-2(x+1)+1}{x+1}$=(x+1)+$\frac{1}{x+1}$-2≥0,即可得出a的范围.若q真,则$\left\{\begin{array}{l}{a≠0}\\{△≥0}\end{array}\right.$,解得a范围.由p且q为假,p或q为真,得p,q中必有一真一假.
解答 解:若P真,由题知:对任意x>-1,$\frac{{x}^{2}}{x+1}$=$\frac{(x+1)^{2}-2(x+1)+1}{x+1}$=(x+1)+$\frac{1}{x+1}$-2≥0,∴a≤0.
若q真,则$\left\{\begin{array}{l}{a≠0}\\{△≥0}\end{array}\right.$,解得a<0或a≥4.
由p且q为假,p或q为真,得p,q中必有一真一假.
∴$\left\{\begin{array}{l}{a≤0}\\{0≤a<4}\end{array}\right.$或$\left\{\begin{array}{l}{a>0}\\{a<0或a≥4}\end{array}\right.$,
解得a=0,或a≥4.
综上所述,a的取值范围是a=0或a≥4.
点评 本题考查了基本不等式的性质、不等式的解法、一元二次方程有实数根的条件、简易逻辑的判断方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
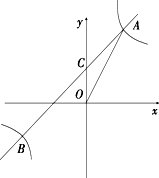 如图,反比例函数y=$\frac{2}{x}$的图象与一次函数f(x)的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.
如图,反比例函数y=$\frac{2}{x}$的图象与一次函数f(x)的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | 30 | N | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com