
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为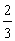 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为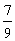 ,求
,求 ;
;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
【解析】(Ⅰ)由已知得,张三中奖的概率为 ,李四中奖的概率为
,李四中奖的概率为 ,且两人中奖与否互不影响.
,且两人中奖与否互不影响.
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为P(X=5)= ×
× ,所以P (A)=1-P(X=5)=1-
,所以P (A)=1-P(X=5)=1- ×
× =
=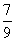 ,所以
,所以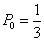 .……6分
.……6分
(Ⅱ)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~B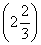 ,X2~B
,X2~B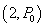 ,
,
所以E(X1)=2× =
=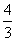 ,E(X2)=2×
,E(X2)=2× ,
,
从而E(2X1)=2E(X1)= ,E(3X2)=3E(X2)=6
,E(3X2)=3E(X2)=6 .
.
若E(2X1) 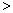 E(3X2),则
E(3X2),则
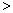 6
6
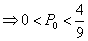 ;
;
若E(2X1) 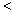 E(3X2),则
E(3X2),则
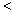 6
6
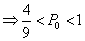 ;
;
若E(2X1) 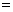 E(3X2),则
E(3X2),则 =6
=6
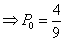 ;
;
综上所述,当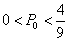 时,他们都选择方案甲进行抽奖,累计得分的数学期望较大;当
时,他们都选择方案甲进行抽奖,累计得分的数学期望较大;当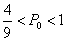 时,他们都选择方案乙进行抽奖,累计得分的数学期望较大;当
时,他们都选择方案乙进行抽奖,累计得分的数学期望较大;当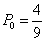 时,他们选择方案甲或方案乙进行抽奖,累计得分的数学期望相等…………13分
时,他们选择方案甲或方案乙进行抽奖,累计得分的数学期望相等…………13分


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
下列说法正确的是 ( )
A. “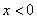 ”是“
”是“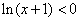 ”的充要条件
”的充要条件
B. “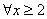 ,
,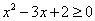 ”的否定是“
”的否定是“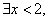
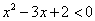 ”
”
C. 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60
D. 在某项测量中,测量结果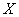 服从正态分布
服从正态分布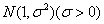 ,若
,若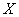 在
在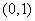 内取值的概率为0.4,则
内取值的概率为0.4,则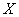 在
在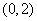 内取值的概率为0.8
内取值的概率为0.8
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l的参数方程是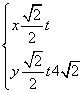 (t是参数),圆C的极坐标方程为ρ=2cosθ+
(t是参数),圆C的极坐标方程为ρ=2cosθ+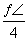 .
.
(1)求圆心C的直角坐标;
(2)由直线l上的点向圆C引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数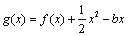 ,函数
,函数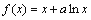 在x=1处的切线与直线
在x=1处的切线与直线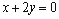 垂直.
垂直.
(1)求实数a的值;
(2)若函数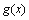 存在单调递减区间,求实数
存在单调递减区间,求实数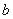 的取值范围;
的取值范围;
(3)设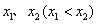 是函数
是函数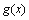 的两个极值点,若
的两个极值点,若 ,求
,求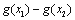 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com