
已知直线l的参数方程是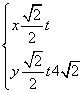 (t是参数),圆C的极坐标方程为ρ=2cosθ+
(t是参数),圆C的极坐标方程为ρ=2cosθ+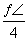 .
.
(1)求圆心C的直角坐标;
(2)由直线l上的点向圆C引切线,求切线长的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
非空集合 关于运算
关于运算 满足:(1)对任意的
满足:(1)对任意的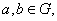 都有
都有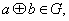 (2)存在
(2)存在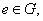 都有
都有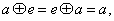 (3) 对任意的
(3) 对任意的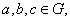 都有
都有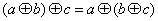 ,则称
,则称 关于运算
关于运算 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①  ={非负整数},
={非负整数}, 为整数的加法。
为整数的加法。
②  ={奇数},
={奇数}, 为整数的乘法。
为整数的乘法。
③  ={平面向量}
={平面向量} 为平面向量的数量积。
为平面向量的数量积。
④ ④ ={二次三项式},
={二次三项式}, 为多项式加法。
为多项式加法。
⑤  ={虚数},
={虚数}, 为复数的乘法。其中
为复数的乘法。其中 关于运算
关于运算 为“融洽集”的是 ( )
为“融洽集”的是 ( )
A.①④⑤ B.①② C.①②③⑤ D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为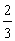 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为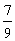 ,求
,求 ;
;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
直线l与圆C:x2+y2-4x+2y+a=0(a<3)相交于A,B两点,弦AB的中点为D(1,0),则直线l的方程为
A. x-y-1=0 B.x+y+1=0 C. x-y+1=0 D.x+y-1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com