
设函数 .
.
(1)若函数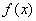 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数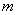 的取值范围;
的取值范围;
(2)若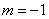 ,试比较当
,试比较当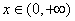 时,
时,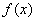 与
与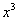 的大小;
的大小;
(3)证明:对任意的正整数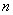 ,不等式
,不等式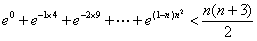 成立.
成立.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
如图所示, 医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后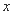 分钟, 瓶内液面与进气管的距离为
分钟, 瓶内液面与进气管的距离为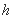 厘米,已知当
厘米,已知当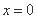 时,
时,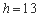 .如果瓶内的药液恰好156分钟滴完. 则函数
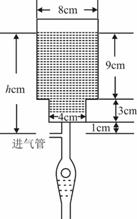
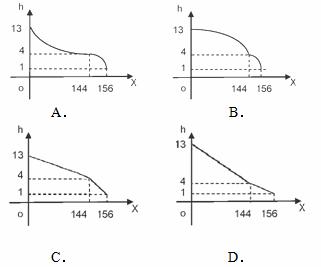
.如果瓶内的药液恰好156分钟滴完. 则函数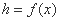 的图像为( )
的图像为( )
查看答案和解析>>
科目:高中数学 来源: 题型:
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为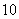 .
.
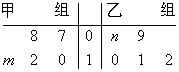
(1)分别求出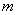 ,
,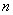 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差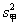 和
和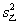 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于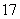 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差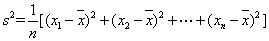 ,其中
,其中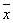 为数据
为数据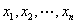 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为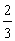 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为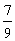 ,求
,求 ;
;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com