练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知函数f（cosx）=cos2x，则f（sin30°）=-$\frac{1}{2}$．

    分析 由题意可得f（sin30°）=f（cos60°）=cos120°，计算可得结果．

    解答 解：∵函数f（cosx）=cos2x，则f（sin30°）=f（cos60°）=cos120°=-$\frac{1}{2}$，
    故答案为：-$\frac{1}{2}$．

    点评 本题主要考查利用诱导公式进行化简求值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

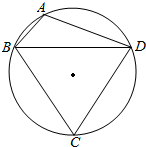    16．某城市在进行规划时，准备设计一个圆形的开放式公园，为达到社会和经济效益双丰收，园林公司进行如下设计，安排圆内接四边形ABCD作为绿化区域，其余作为市民活动区域，其中△ABD区域种植花木后出售，△BCD区域种植草皮后出售，已知草皮每平方米售价为a元，花木每平方米的售价是草皮每平方米售价的三倍，若BC=6km，AD=CD=4km．
    （1）若BD=2$\sqrt{7}$km，求绿化区域的面积；
    （2）设∠BCD=θ，当θ取何值时，园林公司的总销售金额最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知tan（α+β）=5，tan（α-β）=3，求tan2α，tan2β，tan（2α+$\frac{π}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知命题p：方程x2+mx+1=0有两个不相等的负实根，命题q：不等式x2+（m-2）x+1=0无实根，若p或q为真，p且q为假，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

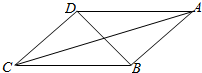    1．如图，在平行四边形ABCD中，已知AB=CD=a，AD=2a，∠DAB=60°，AC∩BD=E，将其沿对角线BD折成直二面角．
    （1）证明：AB⊥平面BCD；
    （2）证明：平面ACD⊥平面ABD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求证：$\frac{si{n}^{2}α}{1+cotα}$+$\frac{co{s}^{2}α}{1+tanα}$=1-sinαcosα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．（1）设f（x）的定义域为R的函数，求证：F（x）=$\frac{1}{2}$[f（x）+f（-x）]是偶函数；G（x）=$\frac{1}{2}$[f（x）-f（-x）]是奇函数．
    （2）利用上述结论，你能把函数f（x）=3x3+2x2-x+3表示成一个偶函数与一个奇函数之和的形式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知不等式loga（1-$\frac{1}{x+2}$）＞0的解集是（-∞，-2），则a的取值范围是（　　）
    A．0＜a$＜\frac{1}{2}$B．$\frac{1}{2}$＜a＜1C．a＞2D．a＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数解析式为f（x）=4•9x+3x+2．
    （1）若已知函数f（x）的定义域为（-1，1），求函数f（x）的值域；
    （2）若已知函数f（x）的值域为[7，+∞），求f（x）的定义域．

    查看答案和解析>>

    同步练习册答案